Разрешающая способность микроскопа

Тогда

Из треугольника:.

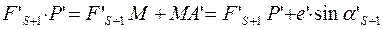и

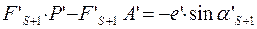
Аналогично получается выражение:

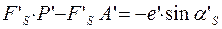
Из приведенного ранее выражения

;

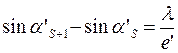
Мы имеем: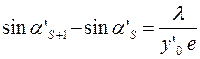

Тогда: ;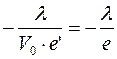

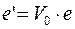
Полученная формула совпадает с формулой геометрической оптики. Однако формула эта может быть нарушена. Пусть в плоскости апертурной диафрагмы перекрыты все нечетные спектры при помощи диафрагмы.

Тогда будем иметь:

,

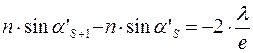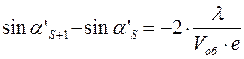
Последняя формула не изменяется:

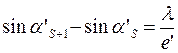
Отсюда получаем:

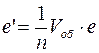
Таким образом, перекрыв спектры первичного изображения через один, мы получаем удвоенную частоту структуры изображения. Вообще говоря, при экранировании некоторых спектров первичного изображения, во вторичном изображении. Вообще говоря, при экранировании некоторых спектров первичного изображения могут возникать так называемые «духи», т.е. такие структурные детали, которые не соответствуют никакая реальность в строении предмета.

В основной формуле решетки: 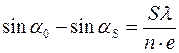, период e входит в знаменатель, следовательно, чем меньше период 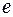, тем больше угол a_S и тем более широким веером расходятся дифрагированные пучки лучей. Но апертурная диафрагма ограничена в размерах, поэтому, чем меньше период e, тем меньше число спектров разных порядков уместится в отверстии апертурной диафрагмы. При малом 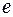наступает момент, когда в отверстии апертурной диафрагмы помещается один спектр. При наличии только одного спектра интерференция не произойдет, и полевая диафрагма будет освещена равномерно. Это значит, что данный период e решетки лежит ниже предела разрешающей способности микроскопа. При определении разрешающей способности следует различать прямое и косое освещение. При прямом освещении изображение источника света нулевого порядка (не разложенное в спектр) возникает у центра апертурной диафрагмы (рис. 6.5.1). Когда решетка с периодом 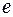находится на пределе разрешения, у краев диафрагмы еще находится половины спектров первого и минус первого порядков. При этом 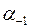должен быть равен апертурному углу микроскопа:

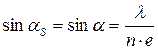
Откуда определяется:

.

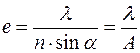При косом освещении решетка освещается пучком параллельных лучей, угол наклона пучка 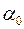равен апертурному углу 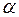микроскопа. В отверстии апертурной диафрагмы у нижнего края получается изображение источника света нулевого порядка (рис. 6.5.2). В этом случае:

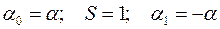
Тогда:

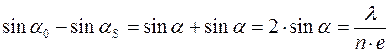и .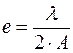

Таким образом, при замене прямого освещения косым, разрешающая способность микроскопа повышается вдвое.

Однако в реальных условиях в микроскопе обычно осуществляется всестороннее освещение, при котором предмет освещается множеством параллельных лучей, проходящих под всевозможными углами к оси в пределах апертуры микроскопа. Этот случай был исследован акад. Рождественским, который получил формулу:

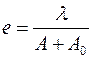
где 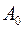- численная апертура конденсора.

Микроскоп должен обладать достаточно большим видимым увеличением, чтобы изображение малого элемента структуры было видно наблюдателю под углом зрения, соответствующим предельному углу разрешающей способности глаза.

Такое увеличение 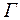микроскопа называется полезным увеличением. Действительно, дальнейшее повышение увеличения будет бесполезным, так как оно не позволит обнаружить мелкие структурные детали предмета, ибо они меньше предельной величины .

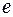Мы имели: 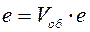. Глаз рассматривает изображение 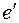под углом 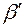через окуляр с определяемым выражением: 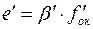, то есть:

Окуляр, в нашем случае, есть лупа, для которой мы имели формулу:

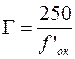
Тогда,

; ;

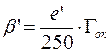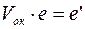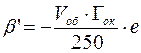
Произведение 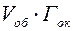видимое увеличение 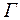микроскопа:

;

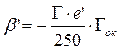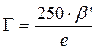
Диаметр выходного зрачка микроскопа часто бывает значительно меньше наименьшего диаметра зрачка глаза, что приводит к понижению его разрешающей способности, а следовательно, к увеличению угла .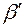

Практически целесообразно принять .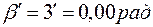

Тогда 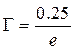( 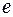в мм); или 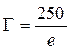( 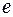в мкм).

Вследствие этого можно утверждать, что полезным является такое увеличение, при котором предмет, находящийся на пределе разрешения, увеличивается до 250 мкм, при этом величина изображения 250 мкм должна измеряться в плоскости, отстоящей от глаза на 250 мм.

Разрешающая способность микроскопа: .

Подставляя это выражение в формулу для 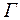, получим:

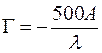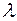( в мкм)

При 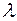= 0.5 мкм, получим известное правило Аббе:

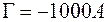
Практически увеличение 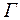микроскопа следует выбирать в пределах от 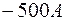до .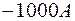

Дата добавления: 2015-06-04