Пример 5

Принципы решения задач на равновесие тела под действием пространственной системы сил.

Принцип решения задач этого раздела остается тем же, что и для плоской системы сил. Установив, равновесие, какого тела будет рассматриваться, заменяют наложенные на тело связи их реакциями и составляют условия равновесия этого тела, рассма­тривая его как свободное. Из полученных уравнений определяются искомые величины.

Для получения более простых систем уравнений рекомендуется оси проводить так, чтобы они пересекали больше неизвестных сил или были к ним перпендикулярны (если это только излишне не усложняет вычисления проекций и моментов других сил).

Новым элементом в составлении уравнений является вычисление моментов сил относительно осей координат.

В случаях, когда из общего чертежа трудно усмотреть, чему равен момент данной силы относительно какой-нибудь оси, рекомендуется изобразить на вспомогательном чертеже проекцию рассматри­ваемого тела (вместе с силой) на плоскость, перпендикулярную к этой оси.

В тех случаях, когда при вычислении момента возникают затруд­нения в определении проекции силы на соответствующую плоскость или плеча этой проекции, реко­мендуется разложить силу на две взаимно перпендикулярные состав­ляющие (из которых одна парал­лельна какой-нибудь координат­ной оси), а затем воспользоваться теоремой Вариньона.

Рама АВ (рис.45) удерживается в равновесии шарниром А и стержнем ВС. На краю рамы находится груз весом Р. Опреде­лим реакции шарнира и усилие в стержне.

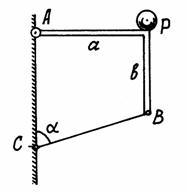
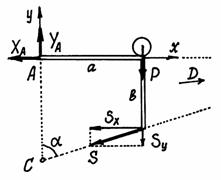
Рис.45

Рассматриваем равновесие рамы вместе с грузом.

Строим расчётную схему, изобразив раму свободным телом и показав все силы, действующие на неё: реакции связей и вес груза Р. Эти силы образуют систему сил, произвольно расположенных на плоскости.

Жела­тельно составить такие уравнения, чтобы в каждом было по одной неиз­вестной силе.

Рекомендуется составлять уравнения моментов относительно трёх точек, точек пересечения линий действия неизвестных сил.

В нашей задаче это точка А, где приложены неизвестные 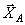и 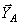; точка С, где пересекаются линии действия неизвестных сил 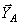и 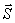; точка D – точка пересечения линий действия сил 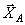и 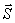. Со­ставим уравнение проекций сил на ось у (на ось х проектировать нельзя, т.к. она перпендикулярна прямой АС).

И, прежде чем составлять уравнения, сделаем еще одно полезное заме­чание. Если на расчётной схеме имеется сила, расположенная так, что плечо её находится непросто, то при определении момента рекоменду­ется предварительно разложить вектор этой силы на две, более удобно направленные. В данной задаче разложим силу 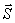на две: 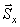и 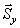(рис.37) такие, что модули их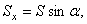

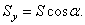
Составляем уравнения: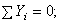

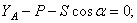
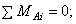
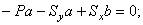
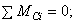
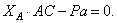
Из второго уравнения находим 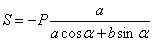. Из третьего 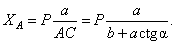И из первого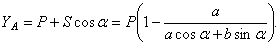

Так как получилось S <0, то стержень ВС будет сжат.

Дата добавления: 2015-06-04