Примеры решения задач произвольная плоская система сил

ПРОИЗВОЛЬНАЯ ПЛОСКАЯ СИСТЕМА СИЛ

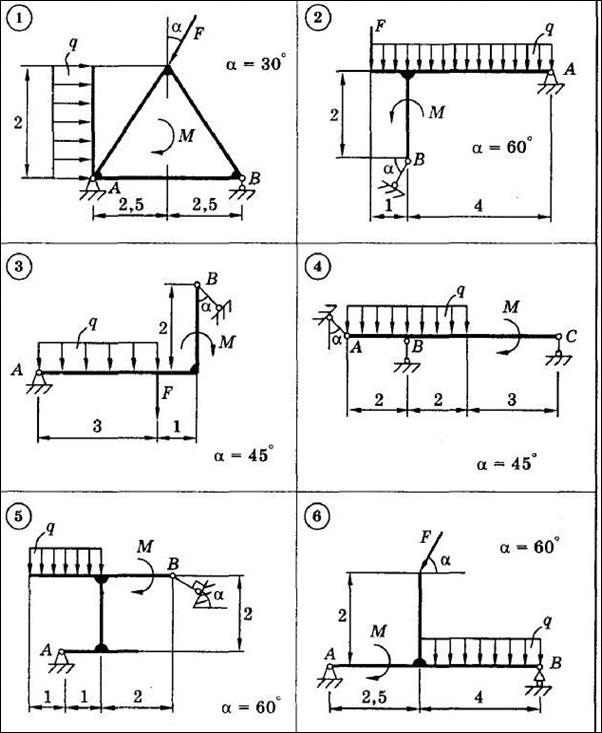
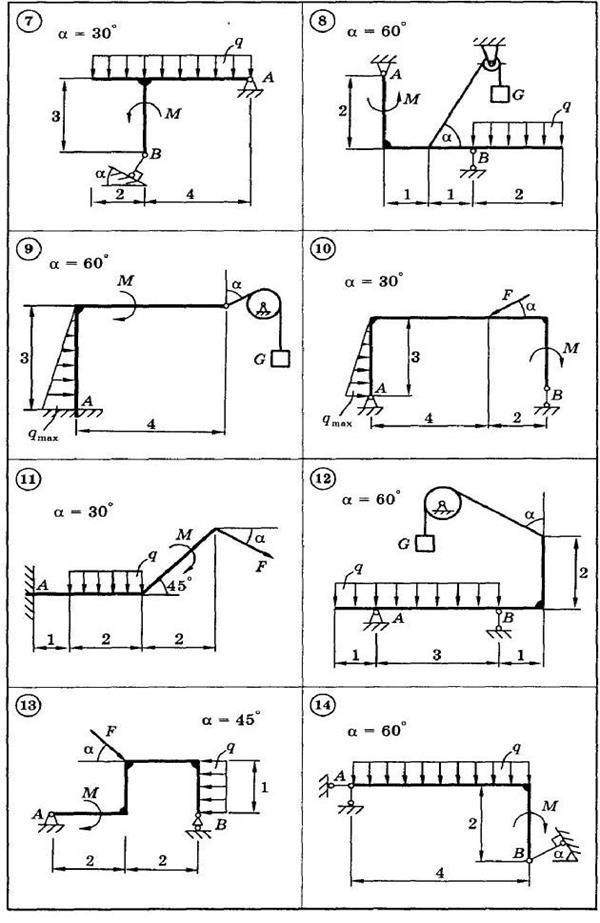
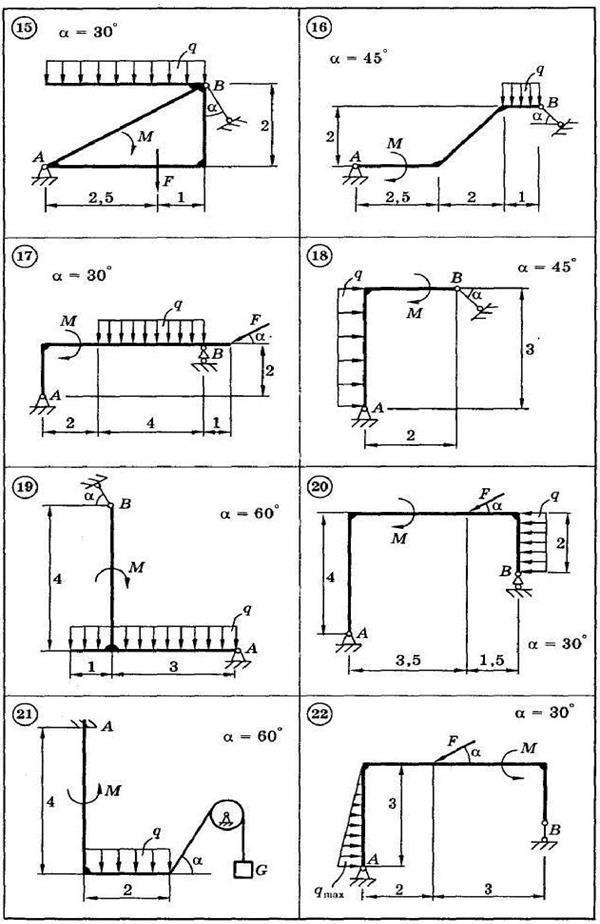
Для представленных на схемах 1—30 тел определить реакции опор. Приведенные на схемах нагрузки имеют следующие величины: вес груза G = 10 кН, сила F = 10 кН, момент пары сил М = 20 кН∙м, интенсивность распределенной силы q = 5 кН/м, а также q_max = 5 кН/м. Размеры указаны в метрах. Весом тела следует пренебречь.

ЗАДАЧА 1

Определить реакции опор А и В однородной балки весом G = 8 кН, находящейся под действием силы F = 6 кН (действующей под углом α = 45°) и равномерно распределенной нагрузки с интенсивностью q = 3 кН/м. Схема балки и геометрические размеры в метрах показаны на рис. 11.

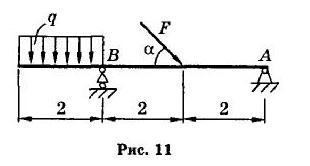
Решение. Воспользуемся принципом освобождаемости от связей, отбросим их и введем соответствующие реакции. В точке В балка имеет скользящую (шарнирно-подвижную) опору, реакция которой R_B имеет известное направление (перпендикулярно опорной поверхности).

Реакция шарнирно-неподвижной опоры в точке А имеет неизвестное направление, и ее следует разложить на составляющие по осям .

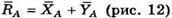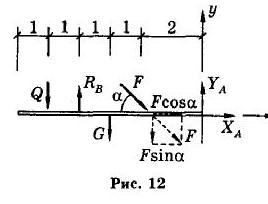
Распределенную по длине l = 2м нагрузку заменим сосредоточенной силой: Q = q l =3 2 =6 кН и приложим в середине участка распределения. Учтем также силу тяжести балки G, приложенную посередине балки.

Составим уравнения равновесия балки в следующей форме: одно уравнение проекций и два уравнения моментов. Такой выбор формы уравнений определяется тем, что в данном случае и в точке А, и в точке В пересекаются по две неизвестные силы. Кроме того, для удобства составления уравнений моментов силу F можно разложить на составляющие по осям: Fcosα и Fsinα и использовать затем теорему Вариньона, согласно которой момент равнодействующей системы сил равен сумме моментов исходных сил.

Уравнения равновесия получаем в виде

Решая эти уравнения с учетом исходных данных, находим

Х_А = -4,24 кН; Rв = 15,6 кН; Y _А = 2,62 кН.

Отрицательный знак у величины Х_А указывает на то, что ее действительное направление противоположно принятому.

Силу, передаваемую через шарнир А, можно вычислить, складывая векторно реакции Х_А и Y_А:

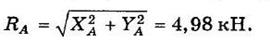
Для проверки правильности решения можно составить, например, сумму проекций сил на ось у и убедиться в том, что она (с небольшой погрешностью, определенной приближенностью вычислений) равна нулю:

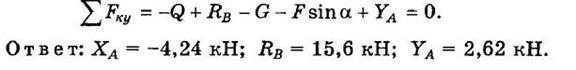
ЗАДАЧА 2

Определить реакции в заделке невесомой консольной балки (рис. 13), находящейся под действием пары сил с моментом М = 4 кН•м и линейно распределенной нагрузки с максимальной интенсивностью q_max = 1,5 кН/м. Длина балки l = 12 м.

Решение. Воспользуемся принципом освобождаемости от связей, отбросим связи и введем реакции, которые для заделки будут представлять собой две составляющие силы реакции по осям Х_А и Y_A и пару с моментом М_A - моментом заделки (рис. 14).

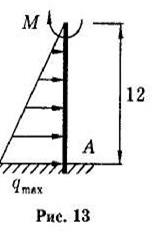
Кроме того, распределенную силу заменим сосредоточенной, равной в данном случае площади треугольника нагрузки:

и проходящей через центр тяжести этого треугольника, то есть на расстоянии 1/3 от основания и 2/3 от вершины (4 м и 8 м).

Для расчетной схемы составляем три уравнения равновесия: Σ F_К=0 на декартовы оси х и у и Σ М_А(F_K)=0 относительно точки А:

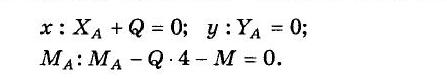
Решая эти уравнения, получаем

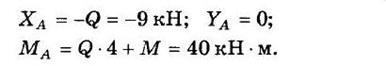
Таким образом, реакция в заделке представлена силой 9 кН, направленной влево, и парой с моментом 40 кН∙м, действующей против часовой стрелки.

Ответ: Х_A = - 9кH; Y_A = 0; M_A = 40 кН•м.

ЗАДАЧА 3

Однородный стержень АВ (рис. 15) длиной 2 1 опирается на гладкий выступ в точке D и удерживается невесомой нитью ОА длиной l. Определить угол φ между линией стержня и горизонтом. Расстояние OD равно l.

Решение. Освободимся от связей и заменим их реакциями (рис. 16):
Из геометрии имеем DE = АK = l sin2φ.

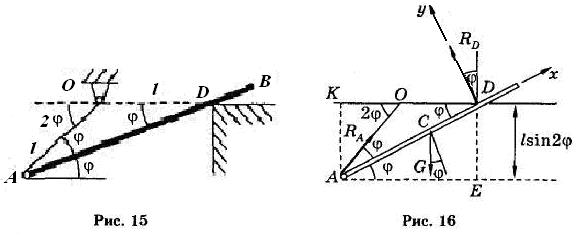
Составляем три уравнения равновесия: Σ F_К=0 на декартовы оси х и у и Σ М_D(F_K)=0 относительно точки D:

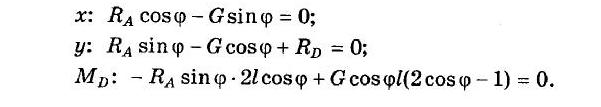
Из первого уравнения следует R_А = G tgφ; подставляем это выражение в третье уравнение, после сокращения получаем -2 sin² + 2 cos²φ - соs φ= 0, или 4 cos²φ - cos φ - 2 = 0.

ЗАДАНИЕ С3

Дата добавления: 2015-06-04