
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоретическая механика
|
|
|
|
РАБОЧАЯ ПРОГРАММА
Введение. Механическое движение как одна из форм движения материи. Предмет механики. Теоретическая механика и ее место среди естественных и технических наук. Механика как теоретическая база ряда областей современной техники.
СТАТИКА ТВЕРДОГО ТЕЛА
Основные понятия и аксиомы статики. Предмет статики. Основные понятия статики: абсолютно твердое тело, сила, эквивалентные и уравновешенные системы сил, равнодействующая, силы внешние и внутренние. Аксиомы статики. Связи и реакции связей. Основные виды связей: гладкая плоскость или поверхность, гладкая опора, гибкая нить, цилиндрический и сферический шарниры, невесомый стержень реакции этих связей.
Система сходящихся сил. Геометрический и аналитический способы сложения сил. Сходящиеся силы. Равнодействующая сходящихся сил. Геометрическое и аналитическое условия равновесия системы сходящихся сил.
Система сил, расположенных на плоскости (плоская система сил). Алгебраическая величина момента силы. Пара сил, ее свойства. Теорема о параллельном переносе силы. Аналитические условия равновесия плоской системы сил. Условия равновесия плоской системы параллельных сил. Теорема Вариньона о моменте равнодействующей. Распределенная нагрузка. Расчет составных конструкций. Расчет ферм.
Произвольная пространственная система сил. Момент силы относительно оси. Приведение пространственной системы сил к простейшему виду. Условия равновесия произвольной пространственной системы сил.
Сцепление и трение тел. Законы Амонтона-Кулона. Коэффициенты сцепления и трения скольжения. Угол и конус трения. Трение качения.
Центр тяжести. Центр тяжести твердого тела и его координаты. Центр тяжести объема, площади и линии. Способы определения положения центров тяжести.
КИНЕМАТИКА
Введение в кинематику. Предмет кинематики. Пространство и время в классической механике. Относительность механического движения. Система отсчета. Задачи кинематики.
Кинематика точки. Векторный способ задания движения точки. Траектория точки. Скорость точки как производная от ее радиус-вектора по времени. Координатный способ задания движения точки в прямоугольных декартовых координатах. Определение траектории точки. Определение скорости и ускорения точки по их проекциям на координатные оси.
Естественный способ задания движения точки. Оси естественного трехгранника. Алгебраическая величина скорости точки. Определение ускорения точки по его проекциям на оси естественного трехгранника: касательное и нормальное ускорения точки.
Кинематика твердого тела. Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении. Вращение твердого тела вокруг неподвижной оси. Уравнение (закон) вращательного движения твердого тела. Угловая скорость и угловое ускорение тела. Скорость и ускорение точки твердого тела, вращающегося вокруг неподвижной оси. Плоскопараллельное движение твердого тела. Уравнения движения. Определение скоростей точек плоской фигуры.
Сложное движение точки. Относительное, переносное и абсолютное движение. Теорема о сложении скоростей. Теорема Кориолиса.
СПИСОК ЛИТЕРАТУРЫ
Воронков И.М. Курс теоретической механики. М., 1954 и последующие издания.
Гернет М.М. Курс теоретической механики. М., 1970 и последующие издания.
Тарг С.М. Краткий курс теоретической механики. М., 1963 и последующие издания.
Мещерский И.В. Сборник задач по теоретической механике. М., 1970 и последующие издания.
Сборник задач по теоретической механике. / Под ред. К.С.Колесникова. М., 1983.
Сборник задач для курсовых работ по теоретической механике / Под ред. А.А. Яблонского. М., 1972 и последующие издания. (Содержит примеры решения задач.)
Пирогов С.П. Краткий курс лекций по теоретической механике. Тюмень, «Вектор Бук», 2001 г.
КОНТРОЛЬНОЕ ЗАДАНИЕ
СОДЕРЖАНИЕ ЗАДАНИЙ, ВЫБОР ВАРИАНТОВ,
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТ,
ОБЩИЕ ПОЯСНЕНИЯ К ТЕКСТУ ЗАДАЧ
Контрольное задание состоит из четырех задач - С1, С2,К1, К2.
К каждой задаче (кроме К1) дается 10 рисунков и таблица (с тем же номером, что и задача), содержащая дополнительные к тексту задачи условия. Нумерация рисунков двойная, при этом номером рисунка является цифра, стоящая после точки. Например, рис. С1.4- это рис. 4 к задаче С1 и т.д. (в тексте задачи при повторных ссылках на рисунок пишется просто рис. 4). Номера условий от 0 до 9 проставлены в 1-м столбце (или в 1-й строке) таблицы.
Студент во всех задачах выбирает номер рисунка по предпоследней цифре шифра, а номер условия в таблице - по последней; например, если шифр оканчивается числом 46, то берет рис. 4 и условия № 6 из таблицы.
Задание выполняется в отдельной тетради (ученической), страницы которой нумеруются. На обложке указываются: название дисциплины, номер работы, фамилия и инициалы студента, учебный шифр, факультет, специальность и адрес. На первой странице тетради записываются: номер работы, номера решаемых задач и год издания контрольных заданий.
Методические указания по решению задач, входящих в контрольные задания, даются для каждой задачи после изложения ее текста под рубрикой “Указания”; затем дается пример решения аналогичной задачи. Цель примера - разъяснить ход решения, но не воспроизвести его полностью. Поэтому в ряде случаев промежуточные расчеты опускаются. Но при выполнении задания все преобразования и числовые расчеты должны быть обязательно последовательно проделаны с необходимыми пояснениями; в конце должны быть даны ответы.
ЗАДАЧИ К КОНТРОЛЬНЫМ ЗАДАНИЯМ
СТАТИКА
Задача С1
Жесткая рама (рис. С1.0 - С1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена к шарнирной опоре на катках.
На раму действуют пара сил с моментом М=100 Н×м и сила, значение, направление и точка приложения которой указаны в таблице (например, в условиях № 1 на раму действует сила F1 = 10 Н под углом 30° к горизонтальной оси, приложенная в точке К).
Определить реакции связей в точках А и В, вызываемые заданными нагрузками. При окончательных подсчетах принять L =0,5 м.
Указания. Задача С1 - на равновесие тела под действием плоской системы сил. Составляя уравнения равновесия, учесть, что уравнение моментов будет более простым (содержать меньше неизвестных),
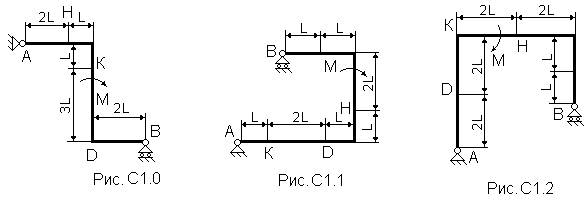
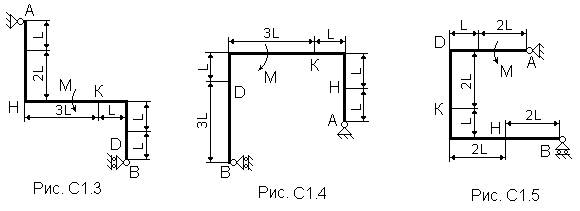
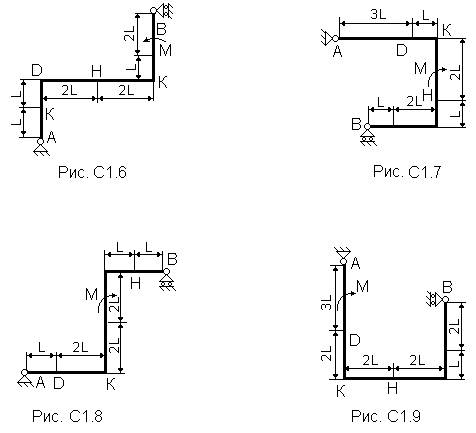
Таблица С1
| Сила | 
| 
| 
| 
| ||||
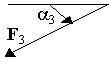
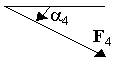
| F1=10 H | F2=20 H | F3=30 H | F4=40 H | |||||
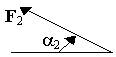
| Номер условия | Точка прилож. | a°1 | Точка прилож. | a°2 | Точка прилож. | a°3 | Точка прилож. | a°4 |
| - | - | D | - | - | ||||
| К | - | - | - | - | ||||
| - | - | K | - | - | ||||
| - | - | - | - | D | ||||
| - | - | D | - | - | ||||
| H | - | - | - | - | ||||
| - | - | - | - | K | ||||
| D | - | - | - | - | ||||
| - | - | H | - | - | ||||
| - | - | - | - | K |
если брать моменты относительно точки, где пересекаются линии действия двух реакций связей (в данном случае относительно точки B). При вычислении момента силы F часто удобно разложить ее на составляющие F / и F //, для которых плечи легко вычисляются, в частности на составляющие, параллельные координатным осям, и воспользоваться теоремой Вариньона; тогда mO(F)=m0(F /)+m0(F //).
Пример С1. Жесткая рама АВС (рис. С1) имеет в точке B неподвижную шарнирную опору, а в точке C - подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.
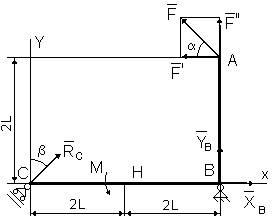
Рис. С1
Дано: F=25 кH, a=60o, b=30°, М=50 кH×м, L =0,5 м.
Определить: реакции в точках B и C, вызываемые действующими нагрузками.
Решение. Рассмотрим равновесие рамы. Проведем координатные оси ХУ и изобразим действующие на раму силы: силу F, пару сил с моментом М и реакции связей XB, YB, RC (реакцию неподвижной шарнирной опоры B изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
Составим три уравнения равновесия плоской системы сил. При вычислении момента силы F относительно точки B воспользуемся теоремой Вариньона, т.е. разложим силу F на составляющие F ’, F’’ (F ’= F cos a, F ’’= F sin a) и учтем, что mB(F)=mB(F ’ )+mB(F '' ). Получим:
1. SFkx = 0, XB + RC sinb - F cosa = 0;
2. SFky = 0, УB + RC cosb + F sina = 0;
3. SmB(Fk) = 0, M - RCcosb×4 L + F cosa × 2 L = 0.
Из этих уравнений находим:
Из (3): 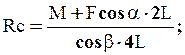
Из (1): XB = - RC sinb + F cosa;
Из (2): YB = - RC cosb - F sina;
Подставив в составленные уравнения числовые значения заданных величин, и решив эти уравнения, определим искомые реакции.
Ответ: XB = - 5,5 кH, YB = 9,6 кH, RC =36,1 кH.
Знаки указывают, что сила XB направлена противоположно показанной на рис.С1.
Задача С2
Рама, состоящая из двух абсолютно твердых ломаных стержней, соединенных между собой шарниром, (рис. С2.0 – С2.9, табл. С2) закреплена в точке А жесткой заделкой, а в точке В прикреплена к шарнирной опоре на катках. Положение шарнира указано в табл.С2.
На раму действуют: пара сил с моментом М=100 Н×м и сила, значение, направление и точка приложения которой указаны в таблице (например, в условиях № 1 на раму действует сила F1 = 10 Н под углом 30° к горизонтальной оси, приложенная в точке D), а также распределенная нагрузка интенсивностью q=20 Н/м, приложенная на участке, указанном в таблице. Если распределенная нагрузка приложена на горизонтальном участке, то она действует вниз, а если на вертикальном, то вправо.
Определить реакции связей в точках А и В, вызываемые заданными нагрузками, а также реакцию внутренней связи. При окончательных подсчетах принять L =0,5 м.
Указания. Задача С2 - на равновесие составных конструкций под действием плоской системы сил. Для определения всех силовых факторов в заделке и реакций шарнирной опоры и внутренней связи необходимо рассмотреть равновесие каждого тела, из которых состоит рама, отдельно, учитывая, что силы взаимодействия между телами равны по величине и противоположны по направлению.
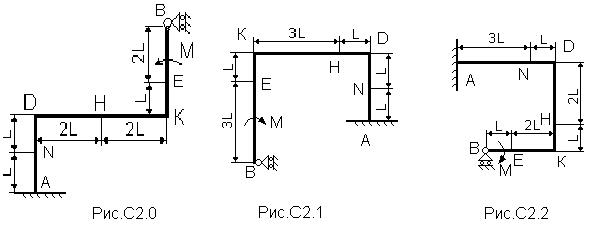
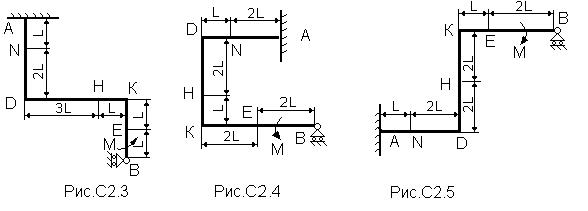
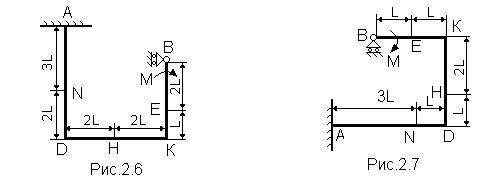
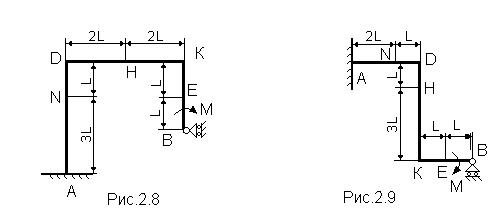
Таблица С2
| Сила |
|

| Точка в которой находится внутренний шарнир | Участок приложения распределенной нагрузки | |||
| F1 = 10 H | F2 = 20 H | ||||||
| № условия | Точка прилож | a°1 | Точка прилож | a°2 | |||
| - | - | N | D | KB | |||
| D | - | - | K | DK | |||
| - | - | K | H | AD | |||
| D | - | - | E | EB | |||
| - | - | D | N | AN | |||
| H | - | - | D | AN | |||
| - | - | E | K | DK | |||
| D | - | - | H | KB | |||
| - | - | H | E | DN | |||
| K | - | - | N | AN | |||
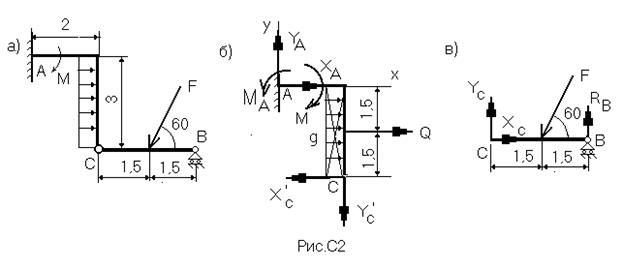
Пример С2. Рама, состоящая из двух изогнутых стержней, соединенных между собой шарниром С, закреплена в точке А жесткой заделкой, а в точке В прикреплена к шарнирной опоре на катках. Определить реакции связей в точках А и В, вызываемые заданными нагрузками, а также реакцию внутреннего шарнира С (рис.С2,а).
Дано: F=20H, M=50 H×M, q=10H/м.
Решение. Рассмотрим равновесие отдельных участков рамы, разделив ее в шарнире С. При этом к левому участку рамы (рис.С2,в) согласно аксиоме отбрасывания связей будут приложены силы реакции опоры В – Rв и реакция в шарнире С, которую разложим на две составляющие – Хс и Ус, а на правую (рис.С2,б) – реакции заделки: силы Ха и Уа, реактивный момент Ма, реакции шарнира С: 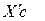 и
и 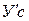 , модули которых равны Хс и Ус, а направление противоположно.
, модули которых равны Хс и Ус, а направление противоположно.
 Составим уравнения равновесия плоской системы сил, приложенной к правой части рамы (рис.С2,в).
Составим уравнения равновесия плоской системы сил, приложенной к правой части рамы (рис.С2,в).
1. 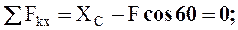
2. 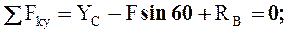
3. 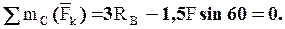
Из (1): 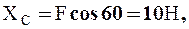
из (3): 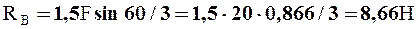 ,
,
из (2):  .
.
Затем составим уравнения равновесия плоской системы сил, приложенной к правой части рамы (рис.С2,б). При этом распределенную нагрузку заменяем равнодействующей Q=3q=30 H, приложенной в центре участка приложения нагрузки.
4. 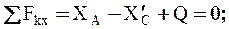
5. 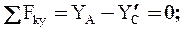
6. 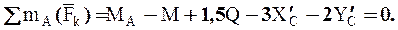
Из этих уравнений находим:
Из (4): 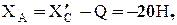
Из (5): 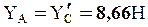 ,
,
Из (6):
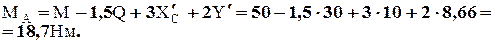
КИНЕМАТИКА
Задача К1
Точка В движется в плоскости xy (табл. К1.1, К1.2). Закон движения точки задан уравнениями: x=f1(t), y=f2(t), где x и y выражены в сантиметрах, t - в секундах.
Найти уравнение траектории точки; для момента времени t1=1c определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость x=f1(t) указана в табл. К1.1, а зависимость y=f2(t) дана в табл. К1.2 (для вар.0 - 2 в столбце 2, для вар.3 - 6 в столбце 3, для вар.7 - 9 в столбце 4). Номер варианта в табл. К1.1 выбирается по предпоследней цифре шифра, а номер условия в табл. К1.2 - по последней.
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение
точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются касательное и нормальное ускорения точки.
В данной задаче все искомые величины нужно определить только для момента времени t1=1с.
Таблица К1.1
| № вар. | x = f (t) | № вар. | x = f (t) |
| x = 4 sin (pt/2) | x = 2t | ||
| x = 3 - 6 sin (pt/2) | x = 2t + 2 | ||
| x = 3 sin (pt/2) - 2 | x = 12 cos (pt/2) | ||
| x = 4 - 2t | x = 6 cos (pt/2) - 2 | ||
| x = 2t + 4 | x = 4 - 8 cos (pt/2) |
Таблица К1.2
| Номер | y = f2 (t) | ||
| условия | Вар. 0 - 2 | Вар. 3 - 6 | Вар. 7 - 9 |
| 9cos(pt/2) | t2 - 2 | -4cos(pt/2) | |
| 3cos(pt/2) | (t + 4)2 | 10sin(pt/2) | |
| 6cos2(pt/2) | 4 + 2t2 | 12sin2(pt/2) | |
| 12cos(pt/2) | 2(t + 1)2 | 4sin(pt/2) | |
| 9cos(pt/2) | 4t2 - 2 | 12cos(pt/2) | |
| -10cos(pt/2) | 3t2 - 2 | 3sin(pt/2) | |
| 8cos(pt/2) | (t + 1)3 | 16sin2(pt/2) | |
| -9cos2(pt/2) | 6t2 | 6cos(pt/2) | |
| 6cos(pt/2) | 2t3 | - 9sin(pt/2) | |
| 2cos(pt/2) | 4t3 | 8cos(pt/2) |
Пример К1. Даны уравнения движения точки в плоскости ху:
x = 2 t, y = t2 (1)
(х, у - в сантиметрах, t - в секундах).
Определить уравнение траектории точки; для момента времени t1 = 1 c найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение. Для определения уравнения траектории точки исключим из заданных уравнений движения время t.
Отсюда находим следующее уравнение траектории точки (парабола, рис. К1):
y = x2 / 4 (2)
Скорость точки найдем по ее проекциям на координатные оси:
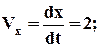
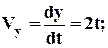
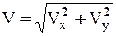
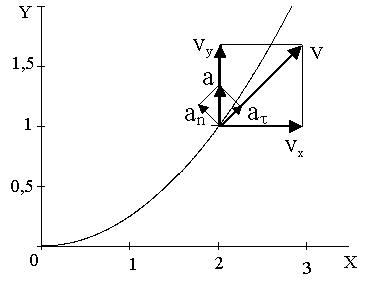
Рис. К1
и при t=1 c: V1x = 2 см/c, V1y = 2 см/c, V1 = 2,83 см/c. (3)
Аналогично найдем ускорение точки:
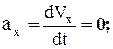
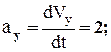
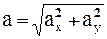
и при t=1 c a1x = 0 см/c2, a1y = 2 см/c2, a1 = 2 см/c2. (4)
Касательное ускорение найдем, дифференцируя по времени равенство V2=V2x+V2y. Получим
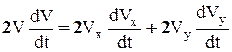 и
и 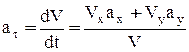 . (5)
. (5)
Числовые значения всех величин, входящих в правую часть выражения (5), определены и даются равенствами (3) и (4). Подставив в (5) эти числа, найдем сразу, что при t1=1 c a1t= 1,4 см/с2.
Нормальное ускорение точки 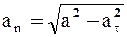 . Подставляя сюда найденные числовые значения a 1 и a 1t, получим, что при t1= 1 а 1n = 1,43 см/с2.
. Подставляя сюда найденные числовые значения a 1 и a 1t, получим, что при t1= 1 а 1n = 1,43 см/с2.
Радиус кривизны траектории r = V2/an. Подставляя сюда числовые значения V1 и a1n, найдем, что при t1=1 c r1 =5,59 см.
Задача К2
Механизм состоит из ступенчатых колес 1, 2, связанных ременной передачей, зубчатой рейки 3 и груза 4, привязанного к концу нити, намотанной на одно из колес (рис. К2.0 - К2.9, табл. К2). Радиусы ступеней колес равны соответственно: у колеса 1- r1 = 2 см, R1 = 4 см, у колеса 2 - r2 = 6 см, R2 = 8 см. На ободьях колес расположены точки А и В.
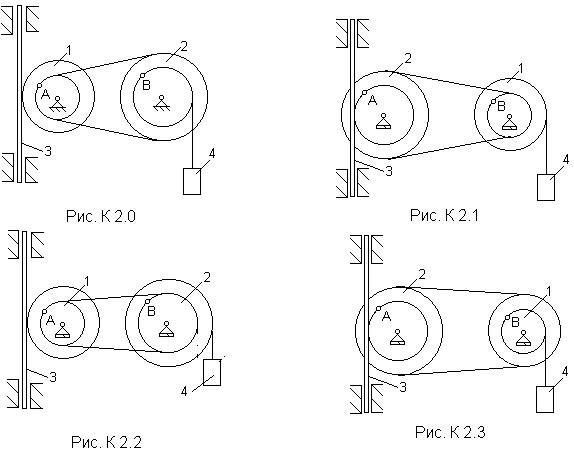
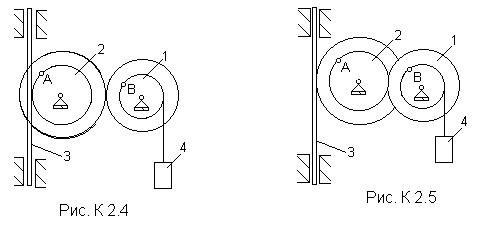
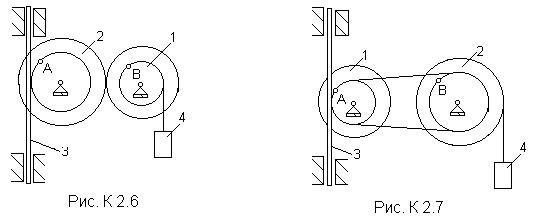
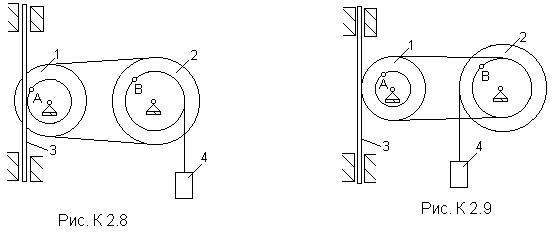
В столбце “Дано” таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где j1(t) - закон вращения колеса 1, s3(t) - закон движения рейки 3, w2(t) - закон изменения угловой скорости колеса 2, v4(t) - закон изменения скорости груза 4 и т.д. (везде j выражено в радианах, s - в сантиметрах, t - в секундах). Положительное направление для j и w - против хода часовой стрелки, для s3, s4 и v3, v4 - вниз.
Определить в момент времени t1 = 2 c указанные в таблице в столбцах “Найти” скорости (v - линейные, w - угловые) и ускорения (а- линейные, e - угловые) соответствующих точек или тел (v4 - скорость груза 4 и т.д.).
Указания. Задача К2 - на исследование вращательного движения
Таблица К2
| Номер | Дано | Найти | |
| условия | скорости | ускорения | |
| s4 = 4(7t - t2) | vA, vB | e1, aA, a3 | |
| v4 = 2(t2 - 3) | vA, vB | e2, aB, a3 | |
| j1 = 2t2 - 9 | v3, w1 | e2, aB, a4 | |
| w2 = 7t - 3t2 | v4, w1 | e2, aB, a4 | |
| j2 = 3t - t2 | v3, w2 | e2, aA, a4 | |
| w1 = 5t - 2t2 | v4, vA | e2, aB, a3 | |
| j1 = 2(t2 - 3t) | v3, w2 | e2, aB, a4 | |
| V3 = 3t2 - 8 | vB, w1 | e1, aA, a4 | |
| s4 = 2t2 - 5t | v3, w1 | e1, aB, a3 | |
| w1 = 8t - 3t2 | v4, vA | e1, aB, a3 |
твердого тела вокруг неподвижной оси. При решении задачи учесть, что, когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны ременной передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы; при этом считается, что ремень по ободу колеса не скользит.
Пример К2. Рейка 1, ступенчатое колесо 2 с радиусами R2 и r2 и колесо 3 радиуса R3, скрепленное с валом радиуса r3, находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К2). Рейка движется по закону s1=f(t).
Дано: R2=6 см, r2=4 см, R3=8 см, r3=3 см, s1=3t3 (s - в сантиметрах, t - в секундах), А - точка обода колеса 3, t1=3 c.
Определить: w3, v4, e3, aA , в момент времени t=t1.
|
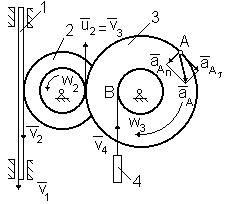
Решение. Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса Ri), через vi, а точек, лежащих на внутренних ободах (радиуса ri), - через ui.
Определяем сначала угловые скорости всех колес как функции времени t. Зная закон движения рейки 1, находим ее скорость:
v1 =  = 9t2. (1)
= 9t2. (1)
Так как рейка и колесо 2 находятся в зацеплении, то v2=v1 или w2R2=v1. Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, u2=v3 или w2r2=w3R3. Из этих равенств находим
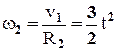 ,
, 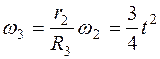 . (2)
. (2)
Тогда для момента времени t1=3 c получим w3=6,75 c-1.
Определяем v4. Так как v4=vB=w3r3, то при t1=3 c v4=20,25 см/c.
Определяем e3. Учитывая второе из равенств (2), получим
e3= 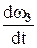 = 1,5t. Тогда при t1=3 c e3=4,5c-2.
= 1,5t. Тогда при t1=3 c e3=4,5c-2.
Определяем a A. Для точки А 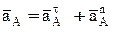 , где численно at A= R3e3, anA =R3w32. Тогда для момента времени t1=3 c имеем
, где численно at A= R3e3, anA =R3w32. Тогда для момента времени t1=3 c имеем
at A= 36 см/c2, anA = 364 см/c2; 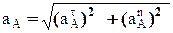 =366 см/c2.
=366 см/c2.
Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис.К2.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 3173; Нарушение авторских прав?; Мы поможем в написании вашей работы!