Момент силы относительно точки и оси

МОМЕНТЫ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ПОНЯТИЕ ПАРЫ СИЛ

Вопросы и задачи для самоконтроля

1. Какое количество независимых уравнений равновесия (в аналитическом виде) можно записать для системы сходящихся сил, действующих на твердое тело, если все они расположены в одной плоскости?

2. Сформулируйте теорему о трех силах, действующих на твердое тело при его равновесии.

3. Какие аксиомы статики были использованы при нахождении равнодействующей системы сходящихся сил?

4. Как должны были бы располагаться лебедь, рак и щука в басне А.Н.Крылова, при условии, что воз оказался в покое на гладкой горизонтальной поверхности?

5. Решите следующие задачи из [2]: 6.8; 6.10.

Рассмотрим силу 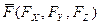, приложенную к твердому телу в точке А(x, y, z).

Очевидно, что сила стремится повернуть тело относительно начала координат. Это воздействие назовем моментом силы относительно точки О; оно характеризуется:

- величиной, пропорциональной как модулю силы, так и наименьшему расстоянию от линии действия силы до начала координат (это расстояние на рис.3.1 обозначено h и называется плечом силы),

- положением в пространстве плоскости, в которой лежат векторы 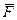и 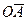(точнее, нормали к этой плоскости),

- направлением вращательного воздействия.

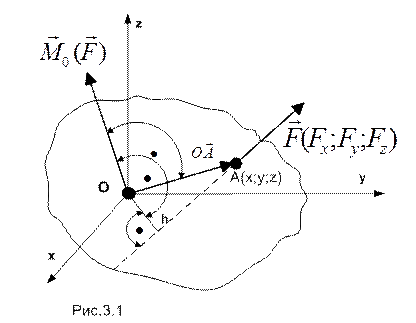
Сопоставим воздействию математическую модель в виде связанного с точкой О вектора, равного

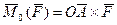(3.1.а)

Очевидно, что принятая математическая модель учитывает все указанные выше характеристики моделируемого вращательного воздействия.

Если известны модуль силы 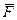и ее плечо относительно точки О, то модуль вектора момента может быть вычислен как:

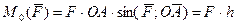(3.1.б)

Момент силы относительно точки О может быть определен и через проекции соответствующих векторов на оси координатной системы, как

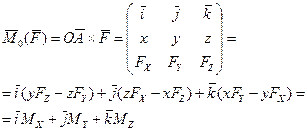
(3.1.в)

Моментом силы относительно оси называется проекция на эту ось момента силы относительно любой точки оси.

В качестве примера разберем вычисление момента силы относительно оси z.

Сначала (см. рис. 3.2) разложим силу на две составляющие – вдоль оси z (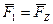) и перпендикулярную оси z ().

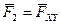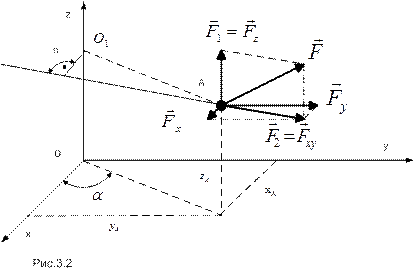
Поскольку состояние тела должно сохраняться при замене равнодействующей на ее составляющие, момент от равнодействующей может быть вычислен, как сумма моментов от ее составляющих, т.е.

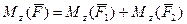(3.2)

Заметим, что приведенное выше соображение в некоторых источниках носит название теоремы Вариньона.

Очевидно, что составляющая 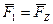стремится сдвинуть тело вдоль оси z, не стремясь повернуть его вокруг оси z (т.е. ее момент относительно оси z равен нулю). Кратчайшее расстояние от линии действия составляющей 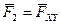до оси z есть h (см. рис. 3.2).

Таким образом,

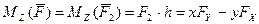(3.3)

что совпадает с проекцией вектора момента на ось z в формуле (3.1.в).

Отметим следующие свойства момента силы:

- момент силы относительно точки не меняется при переносе силы вдоль ее линии действия (т.к. не изменяется плечо силы),

- момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку (т.к. плечо силы равно нулю),

- момент силы относительно оси равен нулю, если сила параллельна оси, либо ее пересекает (т.е. если сила и ось лежат в одной плоскости).

Дата добавления: 2015-06-04