Приведение системы параллельных сил к равнодействующей. Центр параллельных сил

ПРИВЕДЕНИЕ СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ К РАВНОДЕЙСТВУЮЩЕЙ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА И НЕКОТОРЫЕ СПОСОБЫ ЕГО НАХОЖДЕНИЯ

Вопросы и задачи для самоконтроля

1. Сформулируйте лемму о параллельном переносе силы, приложенной к твердому телу.

2. Запишите формулу для вычисления главного вектора системы сил, приложенных к твердому телу, если проекции сил на выбранные координатные оси известны?

3. Запишите формулу для вычисления главного момента системы сил, приложенных к твердому телу, если проекции сил на выбранные координатные оси и координаты точек их приложения сил известны?

4. К какому из частных случаев приводится система сил, расположенных в одной плоскости?

5. К какому из частных случаев приводится система сил, линии действия которых параллельны? (Указание: в случае затруднения с ответом, смотрите параграф 5.1).

6. Для системы из двух сил, изображенной ниже, записать выражения для проекций на ось 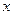главного вектора и главного момента.

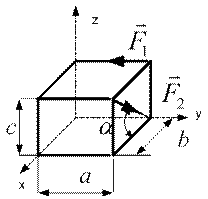
7. Сформулируйте первый инвариант статики.

8. Сформулируйте и запишите формулу для второго инварианта статики.

Рассмотрим систему параллельных сил 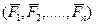, действующих на абсолютно твердое тело. Линии действия сил параллельны некоторой оси L с ортом .

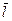Точка приложения каждой силы задана соответствующим радиусом – вектором (см. рис. 5.1).

В этом случае главный вектор будет иметь только проекцию на ось L, а ее величина будет равна алгебраической сумме величин действующих сил, т.е.

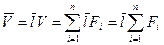(5.1)

где i=1,2,…,n.

Главный момент не будет иметь проекцию на ось L, так как силы системы параллельны этой оси. Прямой угол между главным вектором и главным моментом указывает, согласно изложенному выше, на возможность приведения системы сил к равнодействующей, равной главному вектору. Геометрическую точку, через которую проходит линия действия равнодействующей системы параллельных сил при любом повороте этих сил вокруг точек их приложения, оставляющем силы параллельными друг другу и их взаимную ориентацию, обозначим точкой С и назовем центром системы параллельных сил.

Момент от равнодействующей системы сил должен быть равен сумме моментов от ее составляющих (теорема Вариньона), т.е.

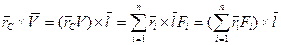(5.2)

Это соображение позволяет рассчитать радиус – вектор точки С (после достаточно простых преобразований с учетом (5.1)), как

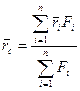(5.3)

Очевидно, что векторной формуле (5.3) соответствуют, в общем случае, три скалярные формулы для вычисления проекций радиуса – вектора точки С на оси выбранной координатной системы. В качестве примера приведем формулу для проекции радиуса - вектора на ось абсцисс декартовой координатной системы:

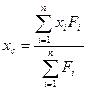(5.4)

Очевидно, что для вычисления проекции на ось ординат (аппликат) в числителе дроби надо сделать соответствующую замену.

Дата добавления: 2015-06-04