Частные случаи приведения систем сил к простейшему виду

Если после приведения пространственной системы сил к выбранному центру О главный вектор и главный момент равны нулю, т.е.

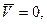
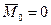(4.1)

- система сил уравновешена. Под действием такой системы сил твердое тело будет находиться в равновесии. Очевидно, что в общем случае двум векторным уравнениям (4.1) соответствуют шесть скалярных уравнений, отражающих равенство нулю проекций этих векторов на оси выбранной координатной системы (например, декартовой).

Если после приведения пространственной системы сил к выбранному центру О главный вектор равен нулю, а главный момент не равен нулю, т.е.

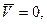
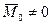(4.2)

- на тело действует результирующая пара сил, стремящаяся его повернуть. Заметим, что в этом случае выбор центра приведения не влияет на результат.

Если после приведения пространственной системы сил к выбранному центру О главный вектор не равен нулю, а главный момент равен нулю, т.е.

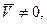
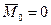(4.3)

- на тело действует равнодействующая системы сил, проходящая через центр приведения и стремящаяся сдвинуть тело вдоль линии своего действия. Очевидно, что соотношения (4.3.) справедливы для всех точек линии действия равнодействующей.

Заметим, что к этому случаю сводится действие системы сходящихся сил, если за центр приведения принять точку пересечения линий действия сил системы (т.к. моменты сил относительно этой точки равны нулю).

Если после приведения пространственной системы сил к выбранному центру О главный вектор и главный момент не равны нулю, а их направления составляют прямой угол, т. е.

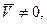
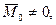
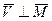(4.4)

то такую систему сил тоже можно привести к равнодействующей, но проходящей через другой центр приведения - точку 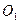. Для выполнения этой операции сначала рассмотрим эквивалентные системы сил, изображенные на рис. 4.2.б и рис. 4.1. Очевидно, что если заменить обозначения (точку В назвать центром О, точку А – центром 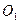), стоящая перед нами задача требует выполнения операции, обратной выполненной в лемме о параллельном переносе силы. С учетом сказанного, точка 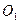должна, во-первых, располагаться в плоскости, перпендикулярной вектору главного момента, проходящей через центр О, и, во-вторых, лежать на линии, параллельной линии действия главного вектора сил и отстоящей от нее на расстоянии h, равном

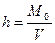(4.5)

Из двух найденных линий следует выбрать ту, для точек которой равен нулю вектор главного момента (момент главного вектора сил относительно нового центра должен быть равен по модулю и противоположен по направлению главному моменту системы сил относительно точки О).

В общем случае после приведения пространственной системы сил к выбранному центру О неравные нулю главный вектор и главный момент составляют между собой не прямой угол (рис.4.5.а).

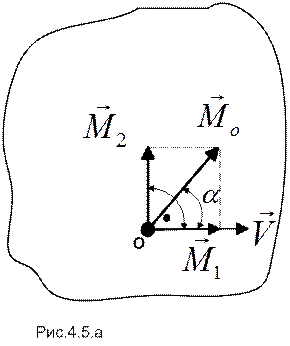
Если главный момент разложить на две составляющие – вдоль главного вектора сил и перпендикулярно ему, то, в соответствии с (4.5), может быть найден такой центр приведения 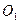, для которого перпендикулярная составляющая главного момента становится равной нулю, а величины и направления главного вектора и первой составляющей главного момента остаются прежними (рис.4.5.б). Совокупность векторов 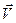и 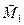называется силовым винтом или динамой.

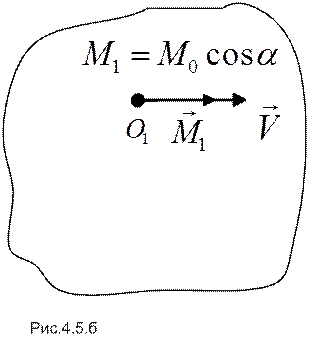
Дальнейшее упрощение не представляется возможным.

Поскольку при такой смене центра приведения изменяется только проекция главного момента на направление, перпендикулярное главному вектору системы сил, остается неизменной величина скалярного произведения этих векторов, т.е.

.

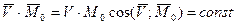Это выражение называется вторым инвариантом

статики.

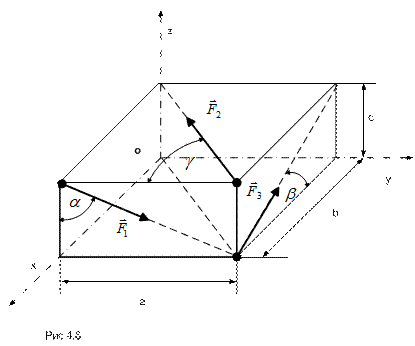
Пример 4.1. На вершины прямоугольного параллелепипеда со сторонами 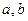и 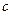действуют силы 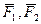и 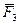(см. рис.4.6). Приняв за центр приведения системы сил начало координат указанной на рисунке декартовой координатной системы, записать выражения для проекций главного вектора и главного момента.

Запишем тригонометрические соотношения для определения углов:

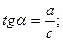
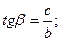
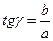
Теперь можно записать выражения для проекций главного вектора и главного момента сил системы:

.

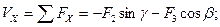
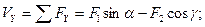
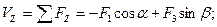
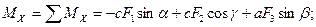
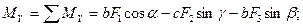
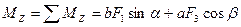Примечание: знание проекций вектора на координатные оси позволит, в случае необходимости, вычислить его величину и направляющие косинусы.

Дата добавления: 2015-06-04