Примеры решения плоских задач статики

Алгоритм решения задач статики

- выделяем объект, равновесие которого будет рассмотрено (точка, тело или механическая система);

- прикладываем к объекту активные (задаваемые) силы;

- освобождаем объект от связей, заменяя их соответствующими реакциями;

- составляем уравнения равновесия системы сил, приложенных к объекту (в векторном или аналитическом виде);

- решаем уравнения, находя неизвестные (параметры равновесного положения и (или) реакции связей).

Пример 6.1 (задача 4.16 из [ 2 ]). Шлюпка висит на двух шлюпбалках, причем вес ее, равный 9.6 кН, распределяется между ними поровну.

Шлюпбалка АВС нижним полушаровым концом опирается на подпятник А и на высоте 1.8 м над ним свободно проходит через подшипник В; вылет шлюпбалки равен 2.4 м. Пренебрегая весом шлюпбалки, определить силы ее давления на опоры А и В.

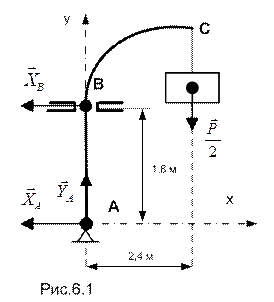
Схематично изобразим шлюпбалку с действующими на нее опорными реакциями (см. рис. 6.1.) и запишем уравнения равновесия полученной плоской системы сил:

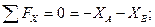
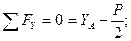
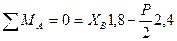
Решив систему относительно неизвестных составляющих опорных реакций, получим:

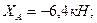
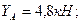
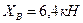
Теперь вычислим силы давления в опорах А и В, как

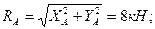
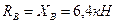
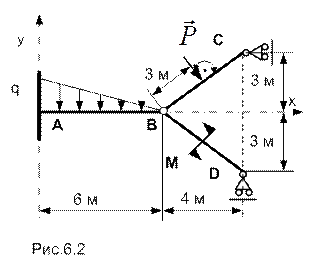
Пример 6.2. Плоская конструкция состоит из трех стержней, соединенных в точке В шарниром. Конец А стержня АВ жестко заделан в вертикальную стену, а концы С и Д стержней ВС и ВД опираются, соответственно, на вертикальную и горизонтальную шарнирно – подвижные опоры. Размеры элементов конструкции и приложенная к ней нагрузка указаны на рис. 6.2.

Составить систему уравнений для нахождения опорных реакций в точках А, Д и С.

Мысленно освободив конструкцию от опор, заменим их действие пятью неизвестными реакциями (две силы и момент в точке А и по одной силе в точках С и Д). Запись трех уравнений равновесия для плоской системы сил, действующей на конструкцию в целом, не позволяет вычислить искомые неизвестные.

Учтем следующее соображение: если конструкция в целом находится в равновесии, то и каждый из ее элементов должен так же находиться в равновесии (т.е. для системы сил, действующих на каждый элемент, можно записать уравнения равновесия).

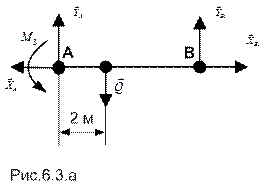
Тогда либо к уравнениям равновесия конструкции в целом добавляют недостающее число уравнений равновесия для ее элементов, либо записывают уравнения равновесия для каждого из элементов, формирующих конструкцию. В рассматриваемом примере выбран второй путь; соответствующие силовые схемы приведены на рис. 6.3.а,б,в (при этом распределенная по линейному закону нагрузка заменена соответствующей равнодействующей).

Для каждого из элементов и узла сочленения (шарнир В), запишем уравнения равновесия:

Стержень АВ:

.

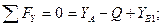
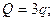
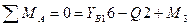Стержень ВС:

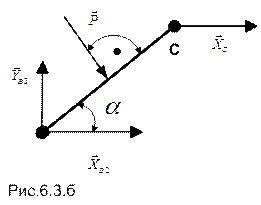
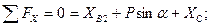
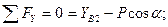
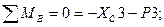
где 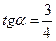=0,75

Стержень ВД:

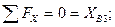
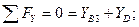
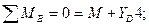
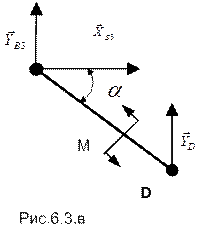
Шарнир В:

.

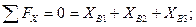
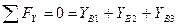Решив систему уравнений, найдем искомые составляющие опорных реакций:

.

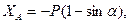
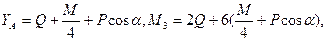
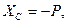
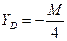Замечание:

- если в узле сочленения соединяются два элемента, то условия равновесия в узле обычно не записываются, а на силовых схемах элементов сразу учитывается 4-я аксиома (третий закон Ньютона) о силах действия и противодействия.

Дата добавления: 2015-06-04