СТАТИКА. Современная техника ставит перед инженерами множество задач, решение которых связано с исследованием механи­ческого движения и механического взаимодействия

Современная техника ставит перед инженерами множество задач, решение которых связано с исследованием механи­ческого движения и механического взаимодействия материальных тел.

Наука о механическом движении и взаимодействии материаль­ных тел и называется механикой

Круг проблем, рассматриваемых в механике, очень велик и с развитием этой науки в ней появился це­лый ряд самостоятельных областей, связанных с изучением меха­ники твердых деформируемых тел, жидкостей и газов

Однако во всех этих областях наряду со специфическими для каждой из них зако­номерностями и методами исследования опираются на ряд основных законов или принципов и используют многие понятия и методы, об­щие для всех областей механики. Рассмотрение этих общих понятий, законов и методов и составляет предмет так называемой теоретиче­ской (или общей) механики

Теоретическая механика — это наука, в которой изучаются общие законы механического движения и механического взаимодействия мате­риальных тел.

Механическим движением называется изменение с течением времени взаимного положения материальных точек в пространстве.

Механическим взаимодействием называется такое взаимодействие материальных тел, которое изменяет или стремится изменить характер их механического движения.

В основе механики лежат законы, называемые законами класси­ческой механики (или законами Ньютона).

Общий метод научных исследований состоит в том, что при рас­смотрении того или иного явления в нем выделяют главное, опреде­ляющее, а от всего остального, сопутствующего данному явлению, абстрагируются.

В результате вместо реального явления или объек­та рассматривают некоторую его модель и вводят ряд абстрактных понятий, отражающих соответствующие свойства этого явления (объекта).

В классической механике такими абстракциями или моделями являются все вводимые исходные положения и понятия. Они учитывают то основное, определяющее, что существенно для рассматриваемого механического движения и позволяет его строго охарактеризовать и изучить.

Это позволяет разработать методы, позволяющие изу­чать с пригодной для практики точностью равновесие и движение реальных объектов, проверяя в свою очередь эту пригодность опытом, практикой.

Роль и значение теоретической механики в инженерном образова­нии определяется тем, что она является научной базой очень многих областей современной техники.

Курс теоретической механики делится на три раздела: статику, кине­матику и динамику.

Статика — это раздел механики, в котором изучаются методы пре­образования систем сил в эквивалентные системы и устанавливаются условия равновесия сил, приложенных к твердому телу.

Кинематика — это раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами, определяющими это движение.

Динамика — раздел механики, в котором изучается движение мате­риальных тел в пространстве в зависимости от действующих на них сил.

Приступая к изучению статики, следует определить основные понятия механики, встречающиеся в этом разделе.

Материальное тело, размеры которого в рассматриваемых кон­кретных условиях можно не учитывать, называют материальной точ­кой. Материальная точка обладает массой и способностью взаимодей­ствовать с другими телами. Например, при изучении движения планет Солнечной системы вокруг Солнца их размерами по сравнению с их расстояниями от Солнца пренебрегают и рассматривают эти планеты кик материальные точки.

Системой материальных точек (или механической системой) на­зывается такая совокупность материальных точек, в которой поло­жение и движение каждой точки зависят от положения и движения других точек этой системы.

В теоретической механике часто рассматриваются тела, расстоя­ния между любыми точками которых остаются неизменными. Такие тела называются абсолютно твердыми.

Способность тел сопротивляться изменению их формы и размеров называется жесткостью. Следова­тельно, тела с абсолютно неизменными размерами и формой следует считать не только абсолютно твер­дыми, но и абсолютно жесткими. Любое абсолютно твердое тело рассматривают как систему материаль­ных точек, неизменно связанных между собой, т. е. лишенных возможности перемещаться относительно друг друга.

Полагая тела абсолютно твердыми, не учитывают деформаций, кото­рые возникают в реальных телах. Это значительно упрощает изучение действия сил на тело и условий, при которых эти силы уравновешиваются.

Условия равновесия сил, при­ложенных к абсолютно твердому телу, используются при изучении действия сил на деформируемое тело с соответствующими допол­нениями.

Твердое тело может нахо­диться в состоянии покоя или движения определенного характе­ра. Каждое из этих состояний условимся называть кинематическим состоянием тела.

Важнейшим понятием в теоретической механике является понятие силы.

Сила — это мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия.

Сила определяется тремя элементами: числовым значением (моду­лем), направлением и точкой приложения.

Сила изображается вектором (рис. 1). Прямая, по которой направлена сила, называется линией действия силы. За единицу силы в Международной системе единиц — СИ (в механике — система МКС) принимается ньютон (Н).

Численно равные силы, но приложенные к телу в разных точках и различным образом направленные, производят на тело не одинаковое по своим последст­виям действие.

Совокупность нескольких сил, действующих на данное тело, назы­вается системой сил.

Системы сил, под действием каждой из которых твердое тело нахо­дится в одинаковом кинематическом состоянии, называются эквива­лентными.

Сила, эквивалентная некоторой системе сил, называется равно­действующей.

Сила, равная по модулю равнодействующей и направленная по линии ее действия в противоположную сторону, называется уравно­вешивающе й.

Система сил, которая, будучи приложенной к твердому телу, нахо­дящемуся в покос, не выводит его из этого состояния, называется системой взаимно уравновешивающихся сил.

Силы, действующие на механическую систему, делятся на две группы: внешние и внутренние силы.

Внешними называются силы, действующие на материальные точки (тела) данной системы со стороны материальных точек (тел), не при­надлежащих этой системе.

Внутренними называются силы взаимодействия между материаль­ными точками (телами) рассматриваемой системы.

Сила, приложенная к телу в какой-нибудь одной его точке, называется с осредоточенной. Силы, действующие на все точки дан­ного объема или данной части поверхности тела, называются распре­деленными.

Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые в механике рассматривают как сосредоточенные, представля­ют собой посуществу равнодействующие некоторых систем распределенных сил.

В частности, рассматриваемая в механике сила тяжести, дейст­вующая на данное твердое тело, представляет собой равнодейст­вующую сил тяжести, действующих на его частицы. Линия действия этой равнодействующей проходит через точку, называемую центром тяжести тела.

Задачами статики являются: 1) преобразование систем сил, дей­ствующих на твердое тело, в системы им эквивалентные, в частно­сти приведение данной системы сил к простейшему виду; 2) опреде­ление условий равновесия систем сил, действующим на твердое тело.

Решать задачи статики можно или путем соответствующих гео­метрических построений (геометрический и графический методы), или с помощью численных расчетов (аналитический метод). В курс будет главным образом применяться аналитический метод, однако, следует иметь в виду, что наглядные геометрические построения иг­рают при решении задач механики чрезвычайно важную роль.

Аксиомы статики.

Для изучения курса статики твердого тела рассмотрим аксиомы, лежащие в основе этого курса. Эти аксиомы сформулированы на основе наблюдения и изучения окружающих нас явлений реального мира. Некоторые основные законы механики Галилея — Ньютона являются одновременно и аксиомами статики.

1. Аксиома инерции. Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно.

Аксиома инерции выражает установленный Галилеем закон инерции.

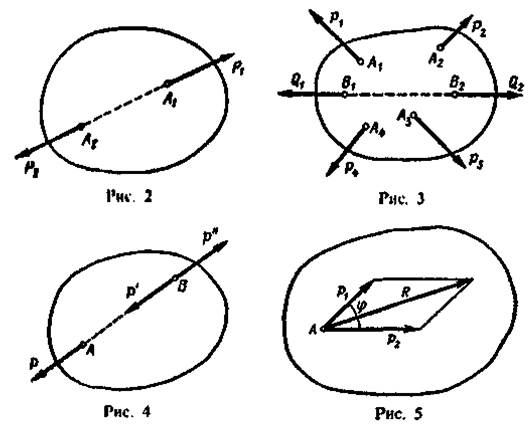
2. Аксиома равновесия двух сил. Две силы, приложенные к твердому телу, взаимно уравновешиваются только в том случае, если их модули равны и если они направлены по одной прямой в противоположные стороны (рис. 2).

3. Аксиома присоединения и исключения уравновешивающихся сил. Действие системы сил на твердое тело не изменится, если к ней присоединить или из нее исключить систему взаимно уравновешивающихся сил.

Пусть, например, к твердому телу приложены силы Р1; Р2, Р3 и Р4, под действием которых тело находится в покое или совершает какое-то движение (рис. 3). Приложим к телу две равные противоположно направленные силы Q1, и Q2, которые взаимно уравновешиваются.

Если тело в покое, то оно сохранит его; если тело в движении, то оно будет двигаться под действием новой системы сил тик же, как под действием сил P1 P2, Р3, Р4, т. е. новая система сил эквивалентно прежней.

Это же произойдет, если из заданной системы сил, приложенных к твердому телу, исключить взаимно уравновешивающиеся силы, входящие в ее состав.

Следствие. Не изменяя кинематического состояния абсолютно твердого тела, силу можно переносить вдоль линии ее действия, сохраняя неизменным ее модуль и направление.

Предположим, что к твердому телу в топке А приложена сила Р (рис. 4). Приложим в точке В две силы Р' и Р", равные по модулю силе Р и направленные по линии ее действия в противоположные стороны. Затем отбросим силы Р и Р", как взаимно уравновешивающиеся. Тогда к телу в точке В будет приложена сила Р' = Р, эквивалентная силе Р в точке А:

Таким образом, силу можно переносить в любую точку по линии действия, не изменяя ее модуля и направления. Поэтому в статике твердого тела сила рассматривается как скользящий вектор.

Данный результат справедлив только для сил, действующих на абсолютно твердое тело. При инженерных расчетах им можно пользоваться лишь тогда, когда определяются условия равновесия той или иной конструкции и не рассматриваются возникшие в ее частях внутренние усилия.

4. Аксиома параллелограмма сил. Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах (рис. 5).

Это положение, хорошо известное из элементарного курса физики, выражается следующим геометрическим равенством:

Модуль равнодействующей силы определяется по следующей формуле

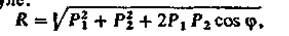
где φ — угол между направлениями сил Р1 и Р2.

Сила R является равнодействующей сил Р1 и Р2. Однако это явление сохраняется только в том случае, если силы приложены в одной точке. В общем случае сила R называется геометрической суммой векторов.

5. Аксиома равенства действия и противодействия. Всякому действию соответствует равное и противоположно направленное противодействие.

Эта аксиома утверждает, что силы действия друг на друга двух тел равны по модулю и направлены по одной прямой в противоположные стороны. Таким образом, в природе не существует одностороннего действия силы. Будучи приложенными к разным телам, эти силы не уравновешиваются.

Аксиома действия и противодействия установлена Ньютоном и известна как один из основных законов классической механики.

Согласно данному закону при взаимодействии две любые части тела действуют друг на друга с равными по модулю и противоположно направленными силами, которые образуют уравновешенную систему сил. Следовательно, для изучения равновесия тела необходимо учитывать только внешние силы.

6. Аксиома сохранения равновесия сил, приложенных к деформирующемуся телу при его затвердении. Равновесие сил, приложенных к деформирующемуся телу, сохраняется при его затвердении.

Из этой аксиомы следует, что условия равновесия сил, приложенных к абсолютно твердому телу, должны выполняться и для сил, приложенных к деформирующемуся телу. Однако в случае деформирующегося тела эти условия необходимы, но не достаточны. Так, например, условие равновесия двух сил, приложенных к твердому стержню на его концах, состоит в том, что силы равны по модулю и направлены по одной прямой в противоположные стороны (рис. 6, а, б).

Две уравновешивающиеся силы, приложенные к нити, удовлетворяют этому условию, но при наличии добавочного условия силы должны только растягивать, а не сжимать нить (рис. 6, а).

Дата добавления: 2015-06-04