
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проскальзывания микро- и наночастиц относительно жидкой матрицы
|
|
|
|
Диссипация акустической энергии микро- и нано- дисперсных систем за счет относительного смещения фаз
Если частица сферической формы находится в жидкости, совершающей возвратно-поступательные движения, например, вибрации c колебательной скоростью ù = ù0e-iωt, то при различной плотности частицы и жидкости-носителя частица будет перемещаться относительно жидкости со скоростью W. Причиной этого является свойство инерции тел, проявляющееся при ускоренном колебательном движении. В силу этого более плотные тела (частицы) при движении отстают от менее плотных (жидкости).
Выражение силы сопротивления, действующей на шар, имеет вид [12]:
 , (2.60)
, (2.60)
здесь δ = η / ρ - кинематическая вязкость.
Первый член выражения (2.60) представляет собой силу сопротивления Стокса в предположении очень медленных колебаний. Второй член - диссипативная сила, обусловленная ускоренным движением обтекающей шар жидкости. При ω=0 эта формула переходит в формулу Стокса. При больших частотах получим:
 , (2.61)
, (2.61)
Первый член в этой сумме соответствует инерционной силе при ламинарном обтекании шара идеальной жидкостью, второй дает предельное выражение для диссипативной силы.
В теории дисперсных систем, разработанной отечественными учеными С.М. Рытовым, В.В. Владимирским и М.Д. Галаниным (1938 г.), получена формула для расчета относительной скорости частиц в среде 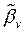 (
(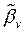 – отношение колебательной скорости взвешенных частиц к скорости окружающей среды) [13
– отношение колебательной скорости взвешенных частиц к скорости окружающей среды) [13
Для достаточно крупных частиц, например в ФС, указанное условие выполняется лишь приближенно. В теории распространения звука в дисперсных системах получена формула для расчета относительной скорости частиц в среде [67,68] 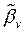 (
(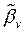 – отношение колебательной скорости взвешенных частиц к скорости окружающей среды):
– отношение колебательной скорости взвешенных частиц к скорости окружающей среды):
 , (2.11)
, (2.11)
где 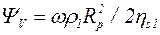 ;
;
 и
и  – плотность и сдвиговая вязкость жидкости-носителя;
– плотность и сдвиговая вязкость жидкости-носителя;
Rp – радиус частиц дисперсной фазы;
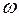 – круговая частота гармонических колебаний;
– круговая частота гармонических колебаний;
 – плотность частиц дисперсной фазы.
– плотность частиц дисперсной фазы.
Выделяя действительную часть выражения (2.11), получаем
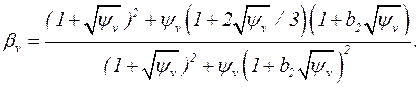
На рисунке 2.3 представлен график зависимости bv(Rp) в полулогарифмическом масштабе. Было принято  =0,8·103 кг/м3,
=0,8·103 кг/м3,  =5,2·103 кг/м3,
=5,2·103 кг/м3,  =1,3·10-3 кг/м·с,
=1,3·10-3 кг/м·с,  =25 МГц. Штриховкой выделена область значений
=25 МГц. Штриховкой выделена область значений 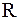 p, характерная для МЖ. Из графика видно, что проскальзывание частиц дисперсной фазы наблюдается начиная с Rp»450 нм и при увеличении Rp до 1–10 мкм становится значительным. Область размеров частиц, соответствующая устойчивой МЖ, лежит в начале горизонтального участка кривой. Колебания намагниченности, обусловленные колебаниями концентрации ФЧ в звуковой волне, описываются уравнениями (2.5) и (2.8).
p, характерная для МЖ. Из графика видно, что проскальзывание частиц дисперсной фазы наблюдается начиная с Rp»450 нм и при увеличении Rp до 1–10 мкм становится значительным. Область размеров частиц, соответствующая устойчивой МЖ, лежит в начале горизонтального участка кривой. Колебания намагниченности, обусловленные колебаниями концентрации ФЧ в звуковой волне, описываются уравнениями (2.5) и (2.8).
 С учетом возможного проскальзывания частиц уравнение непрерывности принимает вид
С учетом возможного проскальзывания частиц уравнение непрерывности принимает вид  , где
, где  – смещение частиц из положения равновесия. Поскольку при гармоническом процессе
– смещение частиц из положения равновесия. Поскольку при гармоническом процессе  ,
,  , то
, то  . Поэтому приращение намагниченности
. Поэтому приращение намагниченности  можно записать так:
можно записать так:
 .
.
Действительная часть последнего выражения при линейной зависимости M(n) имеет вид
 .
.
С учетом конечности времени релаксации получаем:
 .
.
Амплитуду колебаний намагниченности находим из следующего выражения:
 .
.
Принимая, что статическая намагниченность описывается формулой Ланжевена, получим
 . (2.12)
. (2.12)
В области низких частот (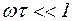 )
)
 . (2.13)
. (2.13)
Выражения (2.12) и (2.13) отличаются от (2.8) множителем  при функции Ланжевена.
при функции Ланжевена.
 Процесс проскальзывания частиц в МЖ может усиливаться за счет агрегирования магнитных частиц в присутствии магнитного поля [18, 45, 47, 126-130]. В тех случаях, когда агломерация приводит к образованию магнитных цепочек, вытянутых преимущественно вдоль поля, становится существенным направление обтекания этих цепочек жидкостью.
Процесс проскальзывания частиц в МЖ может усиливаться за счет агрегирования магнитных частиц в присутствии магнитного поля [18, 45, 47, 126-130]. В тех случаях, когда агломерация приводит к образованию магнитных цепочек, вытянутых преимущественно вдоль поля, становится существенным направление обтекания этих цепочек жидкостью.
При распространении звуковой волны вдоль цилиндрического столба намагниченной жидкости возмущение намагниченности будет неоднородным по длине цилиндра даже при достижении магнитного насыщения [54].
ЗАДАЧА:
15. Процесс «проскальзывания» частиц относительно жидкой матрицы при быстропеременном возвратно-поступательном течении характеризуется параметром 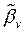 (отношение колебательной скорости взвешенных частиц к скорости окружающей среды):
(отношение колебательной скорости взвешенных частиц к скорости окружающей среды):
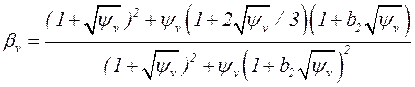 ,
,
где 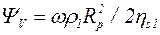 ;
;  – плотность частиц дисперсной фазы.
– плотность частиц дисперсной фазы.
 ;
;  ;
;  и
и  – плотность и сдвиговая вязкость жидкости-носителя;
– плотность и сдвиговая вязкость жидкости-носителя;
Rp – радиус частиц дисперсной фазы;
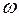 – круговая частота гармонических колебаний.
– круговая частота гармонических колебаний.
Произвести оценку 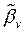 для дисперсных систем с Rp =5 нм и Rp =5 мкм;
для дисперсных систем с Rp =5 нм и Rp =5 мкм;  =0,8·103 кг/м3,
=0,8·103 кг/м3,  =5,2·103 кг/м3,
=5,2·103 кг/м3,  =1,3·10-3 кг/м·с,
=1,3·10-3 кг/м·с,  =25 МГц.
=25 МГц.
 1.11.4.2 Добавочное поглощение ультразвука в герерогенной системе за счет относительного смещения фаз
1.11.4.2 Добавочное поглощение ультразвука в герерогенной системе за счет относительного смещения фаз
Различная плотность компонент дисперсной системы обусловливает их относительное движение при распространении звуковой волны. Благодаря вязкости жидкости-носителя движение частиц относительно среды будет сопровождаться трением, стремящимся уравнять скорости среды и частиц. Процесс обмена импульсом между различными частицами среды протекает с запаздыванием относительно звуковой волны, что приводит к добавочному поглощению звука [67, 68, 156, 157]. Для добавочного поглощения, обусловленного данным процессом, в работах В.В. Владимирского [68] и С.М. Рытова, В.В. Владимирского, М.Д. Галанина [67] выведена формула
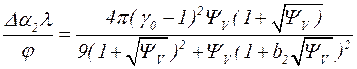 , (4.2)
, (4.2)
где  ,
,  .
.
Зависимость добавочного поглощения от радиуса частицы представлена графически на рисунке 4.1.
Расчет добавочного поглощения в обычных эмульсиях выполняется по формуле [156, 158]
 ,
,
которая является частным случаем выражения (4.2) при 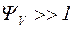 ; к исследуемым средам она не пригодна, значения
; к исследуемым средам она не пригодна, значения  , рассчитанные по этой формуле, имеют порядок 103–104, из чего можно было бы сделать вывод, что распространение звука в такой среде вообще невозможно. Причина непригодности этой формулы к МЖ состоит в том, что для них
, рассчитанные по этой формуле, имеют порядок 103–104, из чего можно было бы сделать вывод, что распространение звука в такой среде вообще невозможно. Причина непригодности этой формулы к МЖ состоит в том, что для них  принимает значения 10-6 – 10-4. В случае
принимает значения 10-6 – 10-4. В случае  формула (4.2) преобразуется так:
формула (4.2) преобразуется так:
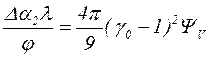 . (4.3)
. (4.3)
Применительно к МЖ в формуле (4.3) необходимо совершить переход от 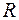 к
к  и одновременно заменить
и одновременно заменить  на
на  , а
, а 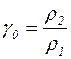 на
на  . С учетом сказанного формула (4.3) принимает следующий вид:
. С учетом сказанного формула (4.3) принимает следующий вид:
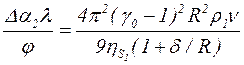 .
.
Полагая r2 =5210 кг/м3 (дисперсная среда – магнетит) и учитывая введенные ранее числовые значения величин, входящих в это соотношение, получим 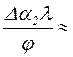 3,7ּ10-2.
3,7ּ10-2.
ЗАДАЧА:
16. В неограниченной жидкости в результате «проскальзывания» частиц будет наблюдаться дисперсия скорости звука – с(ν). При этом относительное приращение скорости дается выражением:
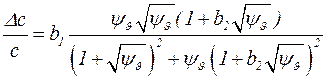 ,
,
где  , (остальные обозначения приведены в условии задачи №20). Рассчитать Δс/с для трех значений ν: 10 кГц; 10 МГц и 50 МГц.
, (остальные обозначения приведены в условии задачи №20). Рассчитать Δс/с для трех значений ν: 10 кГц; 10 МГц и 50 МГц.
17. Процесс обмена импульсом между различными частицами среды протекает с запаздыванием относительно звуковой волны, что приводит к добавочному поглощению звука. Для добавочного поглощения, обусловленного относительным движением фаз, выведена формула
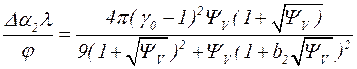 , (4.2)
, (4.2)
где  ,
,  ,
,  .
.
Упростить эту формулу применительно к нанодисперсной системе частиц, например, - к магнитной жидкости. (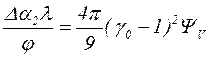 )
)
18. По полученной формуле произвести оценку добавочного поглощения  для магнитной жидкости, с параметрами r2 =5210 кг/м3, r1 =850 кг/м3, R = 5 нм, hs1 =0,13×10‑2 кг/м×с и n =25 МГц.
для магнитной жидкости, с параметрами r2 =5210 кг/м3, r1 =850 кг/м3, R = 5 нм, hs1 =0,13×10‑2 кг/м×с и n =25 МГц.
|
|
|
|
|
Дата добавления: 2015-06-25; Просмотров: 604; Нарушение авторских прав?; Мы поможем в написании вашей работы!