Называется производной от функционала f и обозначается

или (29)

Учитывая (26) и (27) имеем

(30)

Легко убедится, что функционал g также является линейным, непрерывным функционалом на пространстве K.

Легко проверить, что выполняются обычные правила дифференцирования, а именно:

- Производная суммы равна сумме производных

(f₁ + f₂) ^/ = f₁^/ + f₂^/ (31)

- Постоянный множитель выносится за знак производной

(a f₁) ^/ = a f ^/, a – const (32)

- Произведение бесконечно дифференцируемой функции a(x) на обобщённую функцию f:

(a(x) f) ^/= a ^/(x) f + a f ^/ (33)

Действительно, мы имеем:

Для нескольких независимых переменных:

Определим для каждой обобщённой функции f её частные производные по каждому из независимых переменных

(34)

Поскольку, результат дифференцирования обобщённой функции есть снова обобщённая функция, можно определить производную любого порядка

и т.д.

Т.о. все обобщённые функции бесконечно дифференцируемы.

Рассмотрим примеры для случая функции одной независимой переменной.

Пример 1. Рассмотрим функцию Хевисайда

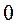
Отвечающий ей функционал обозначим также . Согласно формуле (28) функционал действует на основную функцию так:

(35)

/ по определению “хорошей” или “основной” функции /

Таким образом, в силу определения дельта функции (5)

(36)

Следующая производная

и т.д.

Для смещённой дельта функции из (36) получим

(37)

Пример 2 Пусть f (x) – кусочно-непрерывная функция с кусочно-непрерывной производной f ^/(x), в точках разрывы I рода со «скачками» h₁, h₂, …,

Производная f ^/(x) определена всюду кроме конечного числа точек. Найдём производную от функционала f, соответствующего функции f(x).

Введём функцию:

(38)

Очевидно, что она всюду непрерывна и имеет производную f ^/(x) всюду, кроме конечного числа точек. Как показано ранее (см.(28)), функционал f ^/ соответствует функции f ^/(x), если функции f(x) и f ^/(x) непрерывны. Тогда, из равенства (38), дифференцируя его, получим

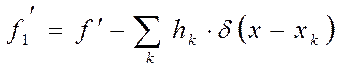
Откуда

(39)

Т.е. если f(x) кусочно-непрерывная функция с кусочно-непрерывной производной, то при дифференцировании, каждая точка разрыва I рода функции f(x) со «скачком» h_k добавляет в выражение производной слагаемое .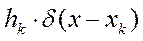

Дата добавления: 2015-06-25