Пример 5. Для случая нескольких независимых переменных

Т.е. ещё раз заметим, что надо внимательно следить за разрывами. Они ведут к дельта функциям.

Пояснение 2:

Исходя из: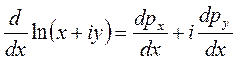

и при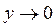

Значит:

или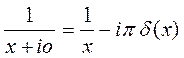

Пояснение 3.

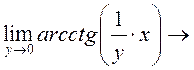укручается и становится ступенькой. В пределе – это функция Хевисайда, только перевёрнутая. При x замена на (- x) мы получим Хевисайд:

.

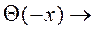
Для непрерывных функций f(x) с кусочно-непрерывными частными производными, дифференцирование соответствующих регулярных функционалов, приводит снова к регулярным функционалам.

Найдем в трехмерном пространстве результат применения оператора Лапласа 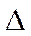к регулярному функционалу, определенному функцией 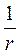, где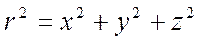

Функция 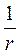гармоническая в любой области, не содержащей начала координат, так, что выражение , при , обращается в нуль (в обычном смысле).

Покажем это. Запишем оператор Лапласа

тогда

;

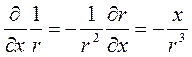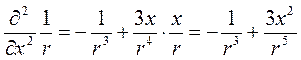
проделав аналогично для других переменных, имеем

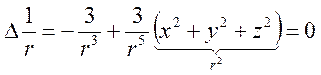
Итак, во всех точках, кроме . В окрестности этой точки надо действовать аккуратно с помощью функционала. Рассматривая оператор Лапласа в пространстве обобщенных функций, находим

Теперь, по формуле Грина для шарового слоя (

dS – есть элемент сферы

Пояснение: формула Грина в общем случае

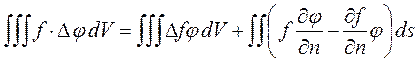
Теперь простые оценки

/

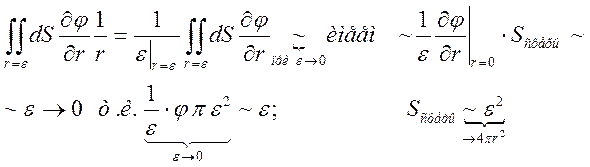
И тогда

т.е. через функционалы

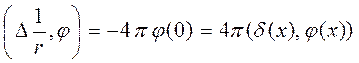
Но отсюда вытекает, что

т.е. вторая производная в трехмерном пространстве равна дельта-функии.

Аналогично, в двумерном пространстве

Пояснение:

где a настолько велико, что вне шара функция 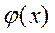тождественно равна нулю.

Дата добавления: 2015-06-25