
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры с решениями
|
|
|
|
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ
О п р е д е л е н и е 10. Смешанным произведением трех векторов  ,
,  и
и 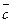 называется число, обозначаемое
называется число, обозначаемое 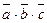 , равное скалярному произведению векторов
, равное скалярному произведению векторов 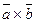 и
и 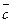 , то есть
, то есть 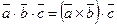 .
.
Свойства смешанного произведения:
1)  ;
;
2) Абсолютная величина смешанного произведения трех векторов численно равна объему параллелепипеда, построенного на этих векторах (рис. 6):
 ç
ç 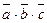 ç.
ç.
 |
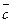





 Рис. 6
Рис. 6
3) Объем тетраэдра (пирамиды, в основании которой лежит треугольник, рис. 7), построенного на векторах  ,
,  и
и 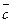 , численно равен:
, численно равен:
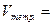
 ç
ç 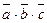 ç.
ç.




 Рис. 7
Рис. 7
4) Три вектора  ,
,  и
и 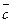 компланарны (параллельны одной плоскости) тогда и только тогда, когда их смешанное произведение равно нулю:
компланарны (параллельны одной плоскости) тогда и только тогда, когда их смешанное произведение равно нулю:
 ,
,  ,
, 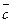 - компланарны
- компланарны 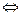
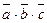 =0.
=0.
5) Если известны координаты векторов
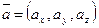 ,
,  и
и 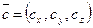 ,
,
то их смешанное произведение вычисляется по формуле:
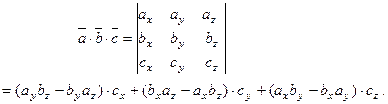 (7)
(7)
П р и м е р 1. Даны точки
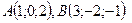 и
и 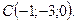
Найти векторы 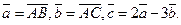
Р е ш е н и е. Найдем векторы 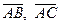 :
:
1) 
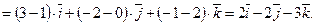
Следовательно, 
2) 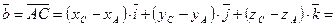
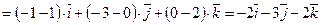 .
.
Следовательно, 
Найдем вектор  :
:
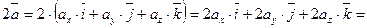
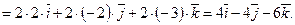
Иначе это действие можно оформить так:
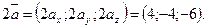
Аналогично:
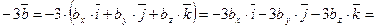
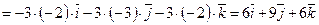 ,
,
откуда 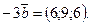
Теперь найдем вектор 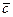 :
:
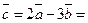
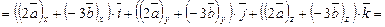
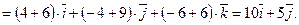
Иначе это действие можно оформить так:
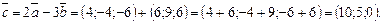
О т в е т: 
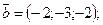
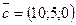 .
.
П р и м е р 2. Даны точки
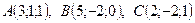 ,
, 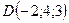 .
.
Показать, что четырехугольник ABCD является трапецией.
Р е ш е н и е. Известно, что у трапеции две противолежащие стороны параллельны (основания трапеции), а две другие – нет.
Для решения данной задачи достаточно убедиться в коллинеарности двух векторов, лежащих на противоположных сторонах четырехугольника ABCD, то есть мы должны показать, что
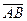 çç
çç 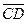 или
или 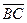 çç
çç 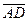 .
.
Найдем эти векторы и рассмотрим отношения их соответствующих координат, поскольку известно, что у коллинеарных векторов координаты пропорциональны.
В данном случае
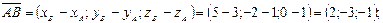


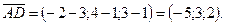
Нетрудно видеть, что 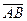 çç
çç 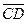 , так как
, так как
 ,
,
Векторы 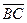 и
и 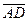 не являются коллинеарными, поскольку их соответствующие координаты не пропорциональны:
не являются коллинеарными, поскольку их соответствующие координаты не пропорциональны:
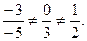
Следовательно, ABCD - трапеция, так как
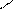
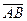 çç
çç 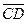 ,
, 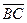 çç
çç 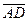 .
.
О т в е т: ABCD - трапеция.
П р и м е р 3. Даны векторы 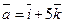 и
и 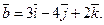 Найти их скалярное произведение.
Найти их скалярное произведение.
Р е ш е н и е. Воспользуемся формулой (3):

О т в е т: 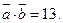
П р и м е р 4. Угол между векторами 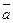 и
и  равен
равен 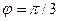 . Известны длины векторов: ç
. Известны длины векторов: ç 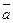 ç=4; ç
ç=4; ç  ç=5. Найти длину вектора
ç=5. Найти длину вектора 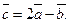
Р е ш е н и е. Воспользуемся тем, что длина вектора равна квадратному корню из скалярного квадрата этого вектора:
ç 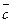 ç=
ç= 
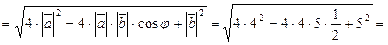
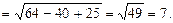
О т в е т: ç 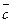 ç=7.
ç=7.
П р и м е р 5. Даны векторы
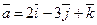 и
и 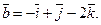
Найти длину их векторного произведения.
Р е ш е н и е. Поскольку векторы заданы координатами, найдем их векторное произведение по формуле (6):
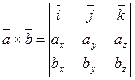 =
= 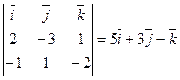 .
.
Найдем теперь длину полученного вектора:
ç 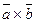 ç=
ç= 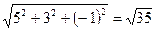 .
.
О т в е т: 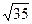 .
.
П р и м е р 6. Даны точки А (2;0;3), В (4;1;2) и С (1;-3;2).
Найти площадь треугольника АВС.
Р е ш е н и е. Известно, что площадь треугольника, построенного на векторах  и
и  , численно равна половине длины векторного произведения ç
, численно равна половине длины векторного произведения ç 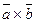 ç.
ç.
Найдем векторы 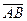 и
и 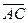 , на которых построен треугольник АВС:
, на которых построен треугольник АВС:
 (4-2;1-0;2-3)=(2;1;-1),
(4-2;1-0;2-3)=(2;1;-1),
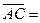 (1-2;-3-0;2-3)=(-1; -3; -1).
(1-2;-3-0;2-3)=(-1; -3; -1).
Следовательно, по формуле (6) вычисляем:
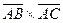 =
= 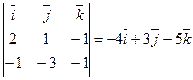 .
.
Отсюда получаем:
ç 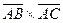 ç=
ç= 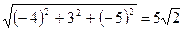 .
.
Поэтому искомая площадь 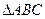 равна:
равна:
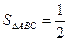 ç
ç 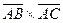 ç=
ç= 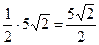 .
.
О т в е т: 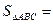
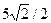 .
.
П р и м е р 7. Показать, что точки А (3;2;1), В (5;1;3), С (4;4;-2) и 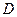 (6;-2;8) лежат в одной плоскости.
(6;-2;8) лежат в одной плоскости.
Р е ш е н и е. Если точки А, В, С и D лежат в одной плоскости, то векторы  и
и 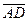 компланарны.
компланарны.
Это можно выяснить, вычислив их смешанное произведение, поскольку известно, что три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Итак, найдем координаты векторов 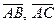 ,
, 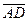 и вычислим по формуле (7) их смешанное произведение:
и вычислим по формуле (7) их смешанное произведение:
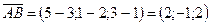 ;
;
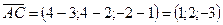 ;
;
 ;
;
 .
.
Следовательно, точки А (3;2;1), В (5;1;3), С (4;4;-2) и
 (6;-2;8) лежат в одной плоскости.
(6;-2;8) лежат в одной плоскости.
О т в е т: точки А, В, С и D лежат в одной плоскости.
|
|
|
|
|
Дата добавления: 2015-06-25; Просмотров: 325; Нарушение авторских прав?; Мы поможем в написании вашей работы!