
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П р и м е р ы
|
|
|
|
1. Найти длину и направление (направляющие косинусы) вектора
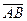 , если
, если 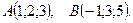
2. Проверить коллинеарность векторов:
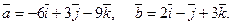
Выяснить, как они направлены относительно друг друга; какой из них длиннее и во сколько раз.
3. Даны точки: 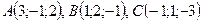 и
и  .
.
Доказать, что ABCD - трапеция.
4. Найти разложение вектора 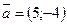 по векторам
по векторам
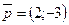 и
и 
5. Найти скалярное произведение 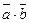 , если
, если

6. Даны векторы:

Найти угол  между векторами
между векторами 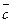 и
и 
7. Векторы 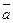 и
и  образуют угол
образуют угол 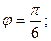 ç
ç 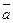 ç=
ç=  ç
ç  ç=1.
ç=1.
Найти угол между векторами 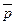 и
и 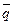 , если
, если
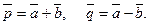
8. Даны четыре точки:
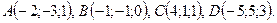
Доказать, что диагонали четырехугольника ABCD перпендикулярны.
9. Даны векторы:

 .
.
Найти проекцию вектора 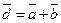 на направление вектора
на направление вектора
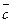 .
.
10. Найти проекцию вектора 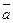 =(5;1;-1) на ось, составляющую
=(5;1;-1) на ось, составляющую
с координатными осями равные острые углы.
11. Известны длины векторов ç  ç=5, ç
ç=5, ç  ç=6, а также угол между ними
ç=6, а также угол между ними 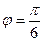 . Найти длину их векторного произведения.
. Найти длину их векторного произведения.
12. Даны векторы:
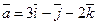 и
и 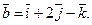
Найти длину и направление (направляющие косинусы) их векторного произведения.
13. Найти длину векторного произведения векторов  и
и  , если известно, что
, если известно, что
ç  ç=10, ç
ç=10, ç  ç=2,
ç=2, 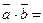 12.
12.
14. Даны два вектора: 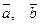 . Известно, что
. Известно, что
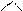 |
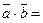 ç
ç  ç=2, ç
ç=2, ç  ç=3,
ç=3, 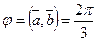 .
.
Найти:
1)  ; 2)
; 2)  .
.
15. Даны точки А (2;3;1), В (4;4;0) и С (3;1;-1). Найти:
1)  3) площадь
3) площадь 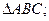
2)  4) высоту
4) высоту  в
в 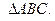
16. Найти смешанное произведение векторов  ,
,  и
и 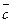 , если:
, если:
1) 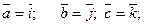
2) 

17. ç 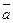 ç=6, ç
ç=6, ç  ç=3, ç
ç=3, ç 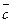 ç=3,
ç=3, 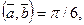
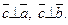 Найти
Найти 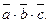
18. Установить, компланарны ли векторы:
1) 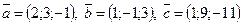 ;
;
2) 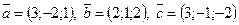 ;
;
3)  .
.
19. Даны точки: А (1;3;5), В (2;-1;0), С (3; -2; -3) и D (0;1; -1). Найти объем пирамиды DАВС и длину ее высоты DO.
20. Доказать, что точки
А (1;1;5), В (2;3;6), С (4; -1;0) и D (3;0;2)
лежат в одной плоскости. Найти площадь четырехугольника АВСD.
21. Найти объем параллелепипеда 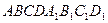 , если известны точки А (2; -1;1), В (5;5;4), С (3;2; -1),
, если известны точки А (2; -1;1), В (5;5;4), С (3;2; -1),  (4;1;3).
(4;1;3).
22. Даны три вершины тетраэдра:
А (2;-1;4), В (0;1;3), С (-5;0;1).
Объем тетраэдра равен 7. Найти его четвертую вершину D, если известно, что она лежит на оси абсцисс.
♦ ♦ ♦
23. Может ли некоторый вектор 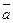 образовать с осями координат углы:
образовать с осями координат углы:
1) 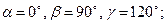
2)  ?
?
24. Найти разложение вектора  по векторам
по векторам
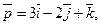
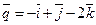 и
и 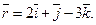
25. Векторы 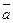 и
и  образуют угол
образуют угол 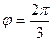 . Зная, что
. Зная, что
ç 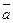 ç=3, ç
ç=3, ç  ç=4, вычислить:
ç=4, вычислить:
1) 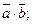 2)
2) 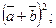
3) 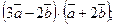
 |
4) ç 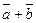 ç; 5)
ç; 5) 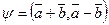 .
.
26. Вектор  коллинеарен вектору
коллинеарен вектору 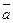 =(2;3;-6) и составляет с осью Oy тупой угол. Найти координаты вектора
=(2;3;-6) и составляет с осью Oy тупой угол. Найти координаты вектора  , если его длина равна 21.
, если его длина равна 21.
27. Проверить, что 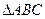 является равнобедренным, если
является равнобедренным, если

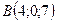 ,
, 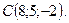
Найти углы треугольника.
28. Даны точки: А (-4;-2;3) и В (5;-2;2). Найти проекцию вектора 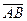 на ось, составляющую с осями Ox и Oy, соответственно, углы
на ось, составляющую с осями Ox и Oy, соответственно, углы 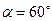 и
и 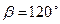 , а с осью Oz тупой угол
, а с осью Oz тупой угол  .
.
29. Даны векторы: 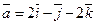 и
и 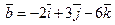 .Найти:
.Найти:

 1)
1) 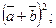 2) ç
2) ç  ç; 3)
ç; 3) 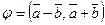 ;
;
4)  .
.
30. Даны точки:  и
и  .
.
Найти:
1) 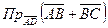 ;
;
2) 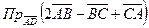 .
.
 |
31. Известно, что ç  ç=3, ç
ç=3, ç  ç=4,
ç=4, 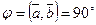 . Найти длины векторов:
. Найти длины векторов:
1)  ; 2)
; 2)  .
.
32. Даны векторы  и
и 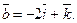 Найти:
Найти:
1) 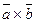 ; 3)
; 3)  ;
;
2) 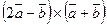 ; 4)
; 4) 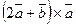 .
.
33. Даны точки: 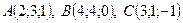 . Найти вектор
. Найти вектор
 .
.
34. Даны вершины треугольника АВС:
 .
.
Найти площадь треугольника АВС и его высоту ВD.
35. Найти вектор 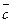 , перпендикулярный векторам
, перпендикулярный векторам  и
и
 , удовлетворяющий условию:
, удовлетворяющий условию:
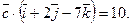
36. Найти смешанное произведение векторов  ,
,  и
и 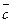 , если:
, если:
1) 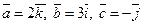 ;
;
2)  .
.
37. Найти объем параллелепипеда, построенного на векторах
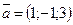 ;
;  и
и  .
.
38. Векторы  ,
,  и
и 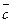 , образующие правую тройку, взаимно перпендикулярны. Зная, что ç
, образующие правую тройку, взаимно перпендикулярны. Зная, что ç  ç=4, ç
ç=4, ç  ç=2, ç
ç=2, ç 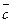 ç=3, вычислить их смешанное произведение
ç=3, вычислить их смешанное произведение 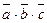 .
.
39. Объем тетраэдра равен 5, три его вершины известны:
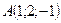 ,
,  и
и  .
.
Найти его четвертую вершину D, если она лежит на оси 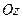 .
.
40. Доказать, что точки
А (1;2;-1), В (0; 1;5), С (-1; 2; 1) и D (2;1; 3)
являются вершинами параллелограмма. Найти углы и площадь этого параллелограмма.
|
|
|
|
|
Дата добавления: 2015-06-25; Просмотров: 437; Нарушение авторских прав?; Мы поможем в написании вашей работы!