Теоремы Лопиталя-Бернулли

Раскрытие неопределённостей типа и

Первая теорема Лопиталя-Бернулли. Пусть для функций 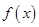и выполнены условия:

1) Функции 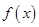и дифференцируемы в промежутке и

2)

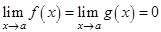
3) Существует предел . Тогда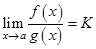

Вторая теорема Лопиталя-Бернулли. Пусть для функций 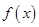и выполнены условия:

1) Функции 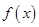и дифференцируемы в промежутке , причем

2)

3) Существует предел . Тогда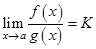

Замечание. Теоремы Лопиталя-Бернулли справедливы и при .

Пример 1. Вычислить предел .

Решение.

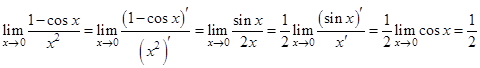
Пример 2. Вычислить предел .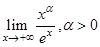

Решение.

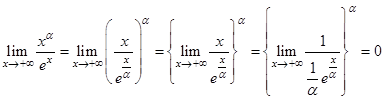
Этот пример показывает, что степенная функция 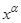даже с очень большим показателем при 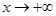растет медленнее, чем показательная функция.

Раскрытие неопределённостей типа

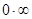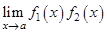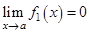Неопределённость типа возникает при нахождении пределов от произведения двух функций, т.е. , где , а 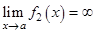. В этом случае произведение 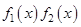записывают так, чтобы можно было воспользоваться первой или второй теоремой Лопиталя-Бернулли.

Пример 3. Вычислить предел .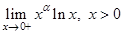

Решение. В данном примере неопределённость 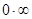, которую сведём к неопределённости и применим вторую теорему Лопиталя-Бернулли.

.

Пример 4. Вычислить предел .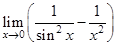

Решение. Имеем неопределённость .

.

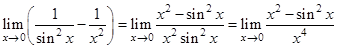Мы воспользовались соотношением при . Применяя далее первую теорему Лопиталя-Бернулли, получим:

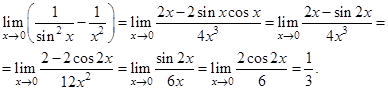
Неопределённости вида 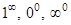возникают при вычислении пределов . Для вычисления данного предела предварительно вычисляют предел 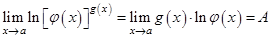. Отсюда следует, что .

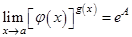Таким образом, раскрытие неопределенностей 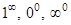сводится к раскрытию соответственно неопределённостей 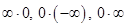, которые в свою очередь могут быть сведены к раскрытию неопределённостей или с применением соответствующих теорем Лопиталя-Бернулли.

Пример 5. Вычислить предел .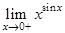

Решение. Имеем неопределённость 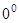. Предварительно вычислим предел 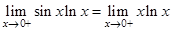. В данном случае мы использовали соотношение 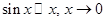, и результат примера 3.

Пример 6. Вычислить предел .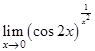

Решение. Имеем неопределённость . Логарифмируя и применяя теорему Лопиталя-Бернулли, получим:

.

Отсюда имеем: .

Найти следующие пределы

6.	14.	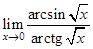22.
7.	15.	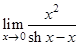23.
8.	16.	24.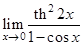
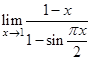
9.	17.	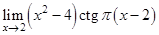25.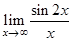
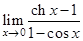
10.	18.	26.
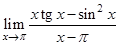
11.	19.	27.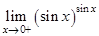
12.	20.	28.
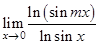
13.	21.	29.

Дата добавления: 2015-06-26