По наклонной плоскости

ТРЕНИЯ СКОЛЬЖЕНИЯ ПРИ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА

ЛАБОРАТОРНАЯ РАБОТА 1.5

Цель работы — изучение динамики поступательного движения твердого тела, экспериментальное определение коэффициента трения скольжения, определение динамических характеристик системы при движении тела с ускорением.

Приборы и принадлежности: трибометр, весы, разновесы, бруски, грузы, секундомер, линейка.

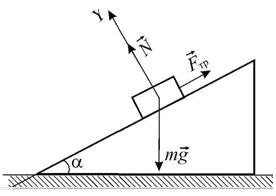
	Теоретические основы работы Сила является мерой взаимодействия между телами. Поэтому мы указываем, что на данное тело действуют силы только тогда, когда на него действуют другие тела. Так на брусок массой 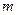, находящийся на наклонной плоскости (рис.1) действуют силы: со стороны Земли — сила тяжести 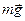,co стороны наклонной плоскости - сила нормальной реакции опоры
Рис. 1. Брусок на наклонной плоскости

и сила трения . Под действием вышеназванных сил брусок может покоиться или скользить по наклонной плоскости.

Состояние покоя бруска описывается уравнением

или

, (1)

где — сила трения покоя.

В проекции на ось X уравнение (1) принимает вид

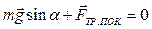
где — угол при основании наклонной плоскости.

Тогда равна проекции внешней силы mg на ось X

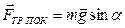(2)

Если изменять угол αпри основании наклонной плоскости, то при некотором предельном значении угла брусок начнет скользить. При этом сила трения покоя принимает свое максимальное значение, равное силе трения скольжения

В свою очередь модуль силы трения скольжения определяется выражением

,

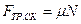где 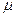— коэффициент трения, N — сила нормальной реакции опоры, а ее направление всегда противоположно скорости движения тела.

Коэффициент трения скольжения зависит от материалов трущихся тел, механической обработки поверхностей, от внешних факторов (температуры, влажности).

Скольжение бруска в соответствии с вторым законом Ньютона описывается уравнением

	, (3)   которое в проекции на ось 7 (рис. 1) дает   .   Тогда выражение для модуля силы трения скольжения принимает вид:   (4)
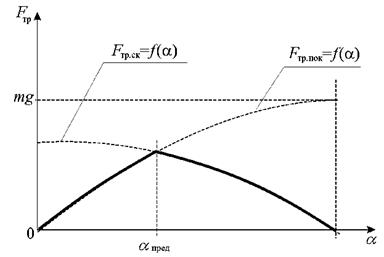
Рис.2. Зависимости F пок и F ск в функции от угла α

На рис.2 представлена зависимость силы трения покоя и скольжения от угла при основании наклонной плоскости.

При 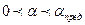брусок действует сила трения покоя, определяемая законом синуса в соответствии с выражением (2). При начинается скольжение бруска. При этом на него начинает действовать сила трения скольжения, определяемая в соответствии с (4) законом косинуса. При

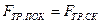или

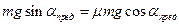
Отсюда получаем связь между углом и коэффициентом трения скольжения

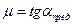, (5)

где - угол наклона плоскости, при котором начинается скольжение бруска.

Рассмотрим систему брусок-груз (3), представленную на рис. 3. Здесь движение бруска 2 происходит под действием груза 3, который связан с бруском нитью 4, переброшенной через блок 5. При определенном

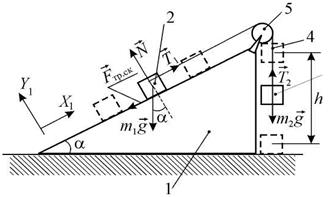
	соотношении между массами бруска и груза, угла α при основании наклонной плоскости и коэффициента трения скольжения. 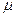брусок будет двигаться вверх по наклонной плоскости с ускорением а. Найдем это соотношение. Движение системы брусок-груз по наклонной плоскости описывается вторым законом
Рис. 3. Система наклонная плоскость- брусок-груз

Ньютона применительно к обоим телам. Для груза:

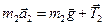, (6)

где - сила натяжения нити, действующая на груз; - ускорение груза. В проекции на ось это уравнение имеет вид:

Для бруска:

,

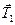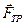где — сила натяжения нити, действующая на брусок; -ускорение бруска - сила трения скольжения.

В проекциях на ос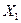и и получаем:

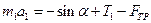(7)

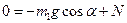(8)

В предположении, что нить и блок не обладают массой, а также нить не растяжима можно записать:

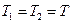
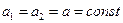(9)

Решая совместно систему уравнений (6), (7), (8), (9), а также, учитывая, что , можно получить формулу для расчета коэффициента трения из

опытов по скольжению бруска по наклонной плоскости:

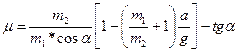(10)

Ускорение а системы брусок груз рассчитываем по данным эксперимента, измерив расстояние h, пройденное грузом 3 и время 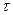движения системы

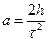(11)

Дата добавления: 2015-06-26