Теория метода. Цель работы:изучение и освоение метода определения модуля сдвига на основе деформации кручения

КРУТИЛЬНЫХ КОЛЕБАНИЙ

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА МЕТОДОМ

ЛАБОРАТОРНАЯ РАБОТА № 1.6 А

Цель работы: изучение и освоение метода определения модуля сдвига на основе деформации кручения.

Приборы и принадлежности: маятник крутильный с грузами; секундомер; штангенциркуль; метровая линейка; микрометр; весы с разновесами.

Деформацию кручения можно классифицировать как неоднородный сдвиг. Поэтому имеется возможность определения модуля сдвига по периоду свободных колебаний крутильного маятника, в котором струна изготовлена из исследуемого материала.

Найдем связь между периодом колебаний крутильного маятника T и модулем сдвига материала струны. Для небольших деформаций имеет место закон Гука: величина упругой деформации 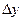прямо пропорциональна действующей силе:

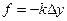(1)

где k – постоянная величина для рассматриваемого твердого тела.

Рассмотрим упругую деформацию сдвига. Пусть на прямоугольный параллелепипед АВДС с высотой действует касательная сила f, под влиянием которой прямоугольный параллелепипед превращается в наклонный параллелепипед 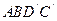(рис.1).

Обозначим величину площади верхнего основания параллелепипеда через S. Сила f действует вдоль верхнего основания по касательной.

Назовем величину этой касательной силы, отнесенной к единице площади, касательным напряжением и обозначим через :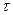

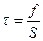
При деформации сдвига смещение 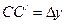является абсолютным сдвигом (рис.1), а отношение абсолютного сдвига 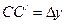к длине ребра

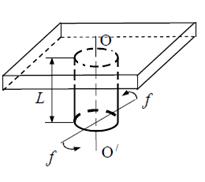
Рис. 1	Рис. 2

параллелепипеда АС = x – относительным сдвигом. Таким образом, относительный сдвиг определяется формулой

Угол сдвига 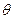есть угол между ребром АС первоначального и ребром деформированного параллелепипеда. При малых деформациях можно считать, что угол сдвига приближенно равен относительному сдвигу:

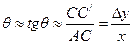
Разделив обе части равенства (1) на S, получим (опустив знак минус)

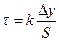
Это выражение можно записать в виде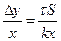

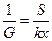Имея в виду, что , и введя обозначение , получим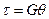

Это есть не что иное, как закон Гука для деформации сдвига: при малых деформациях относительный сдвиг, приближенно совпадающий с углом сдвига 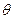, пропорционален касательному напряжению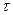

Коэффициент пропорциональности G

между углом сдвига и касательным напряжением является модулем сдвига. Модуль сдвига G зависит от материала тела, которое подвергается деформации.

Пусть к одному концу проволоки или стержня, закрепленного с другого конца, приложена пара сил ff с моментом M (рис.2). Под действием этой пары сил проволока будет закручиваться. Отдельные поперечные сечения проволоки, перпендикулярные ее оси, будут поворачиваться относительно соседних сечений на некоторые углы. Нижнее сечение повернется относительно верхнего на угол 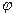, который называется углом кручения.

Тогда по закону Гука, справедливому для малых деформаций, момент пары сил M будет прямо пропорционален углу кручения:

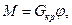
где – модуль кручения. Между модулем кручения и модулем сдвига материала проволоки G имеется простое соотношение

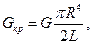
где L – длина проволоки; R – радиус проволоки; G – модуль сдвига

материала проволоки. Если твердое тело, подвешенное на проволоке, закрутить на малый угол 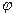и предоставить самому себе, то оно будет вращаться вокруг оси, совпадающей с осью проволоки. При вращении твердое тело будет совершать колебания вокруг первоначального положения равновесия. Такие колебания вращающегося тела являются крутильными колебаниями, а твердое тело – крутильным маятником.

Второй закон Ньютона для вращательного движения в случае крутильного маятника запишется в виде .

Здесь M – вращающий момент относительно оси проволоки; I – момент инерции тела относительно той же оси; 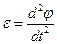– угловое ускорение.

Знак «минус» возник вследствие того, что направление вращающего момента M противоположно направлению углового ускорения .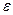

Таким образом, 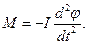При кручении 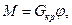, поэтому

Отсюда для крутильного маятника угловое ускорение 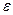прямо пропорционально угловому смещению j и направлено противоположно ему.

Если ускорение тела прямо пропорционально смещению (линейному или угловому) и направлено противоположно ему, то колебания тела являются гармоническими. Коэффициент пропорциональности между ускорением и смещением есть квадрат круговой частоты колебаний. Таким образом, при малых углах кручения крутильный маятник совершает гармоническое колебательное движение. Угловая частота этих колебаний определяется из уравнения

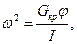
а период полного колебания крутильного маятника определяется

выражением

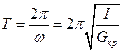
Для периода простого колебания имеем:

(2)

Дата добавления: 2015-06-26