Механика упругих тел

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА И КРУЧЕНИЯ

ЛАБОРАТОРНАЯ РАБОТА № 1.6

Целью работы. Изучение и освоениеэкспериментальных методов определения упругих характеристик материалов: модуля Юнга и модуля сдвига.

Все реальные тела под воздействием сил в той или иной степени меняют свою форму, деформируются.

Абсолютно упругое тело является самой простой моделью, в рамках которой учитывается возможность деформации реальных тел.

Все разнообразие деформаций сводится к двум основным типам, которые можно назвать элементарными. Этими элементарными деформациями являются растяжение (и сжатие) и сдвиг. На рис.1 показано сечение параллелепипеда, жестко закрепленного на массивном жестком столе. Пусть внешняя сила равно мерно распределена по верхней грани параллелепипеда.

При этом, очевидно, такая же по величине, но обратная по направлению сила действует на параллелепипед со стороны стола. Существует два независимых направления силы по отношению к грани, к которой эта сила приложена: нормальное (на рисунке слева) и тангенциальное (на рисунке справа). В первом случае действие силы приводит к сжатию образца, если сила направлена внутрь тела, и к растяжению в противном случае. Количественной характеристикой растяжения (сжатия) является относительное удлинение

Рис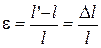.1

. (1)

где l - длина параллелепипеда до приложения нагрузки, l' - во время действия внешней силы. При растяжении e>0, при сжатии e<0. Величину D l называют удлинением образца.

Во втором случае (см. рис.1 справа) действие силы приводит к смещению слоев тела параллельно друг другу вдоль направления действия силы. Сдвиг характеризуется тангенсом угла g. При малых деформациях этот сдвиг мал и можно полагать tgg = g. Исследование деформаций тел сводится к установлению зависимости e и g от приложенной нагрузки. В качестве меры последней выбирается величина f отношения приложенной внешней силы F к площади грани S, на которую эта сила непосредственно действует: f = F / S.

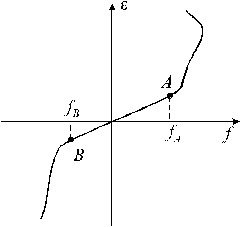
Рис. 2

Характерные результаты экспериментов по растяжению-сжатию образцов представлены на рис.2. Участок кривой АB соответствует так называемым упругим деформациям.

Особенность их в том, что при снятии нагрузки меньшей f_A (при растяжении) или f_B (при сжатии) деформации исчезают. Если внешняя сила превысит предел упругости f_A (f_B) деформации станут неупругими. Т.е. при снятии нагрузки всегда будет иметь место некоторая остаточная деформация. Легко сообразить, что в области неупругих деформаций, нет однозначной зависимости между величиной приложенной нагрузки и величиной деформации. Такую ситуацию весьма затруднительно описать теоретически.

Для упруго деформированного тела согласно закону Гука имеет место однозначная зависимость между приложенной нагрузкой и возникающей деформацией, которая в случае малых деформаций линейна:

f _n= E e, f _t= G g, (2)

где E - модуль Юнга (модуль растяжения), G - модуль сдвига.

Модель абсолютно упругого тела предполагает, что подобная линейная зависимость имеет место при любой деформации.

На практике для характеристики упругих свойств материалов наряду с модулем Юнга вместо модуля сдвига используют коэффициент Пуассона. Введение последнего основано на том факте, что любое сжатие или растяжение сопровождается изменением поперечных приложенной силе размеров образца (см. рис. 3). По определению коэффициент Пуассона

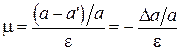. (3)

	Знак минус в этом определении обусловлен тем обстоятельством, что сжатие (e<0) всегда поперечных размеров тела (D a >0), а растяжение (e>0) - уменьшением (D a <0). Таким образом, коэффициент Пуассона сопровождается увеличением положительная безразмерная величина. Так как энергия упругих деформаций положительная величина, можно показать, что
Рис. 3

m<1/2, (4)

и имеет место связь

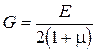(5)

Таким образом,

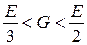(6)

Дата добавления: 2015-06-26