Измерение модуля Юнга из изгиба

ТЕОРИЯ МЕТОДА

ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ПО ИЗГИБУ БАЛКИ

ЛАБОРАТОРНАЯ РАБОТА № 1.6 Б

Приборы и принадлежности: линейка, индикатор, штангенциркуль, набор гирь, балки, опоры.

Изгиб классифицируется как неоднородное растяжение-сжатие. Получим формулу, связывающую параметры изгиба и модуль Юнга.

Рассмотрим изгиб бруса (балки) произвольного сечения, постоянного по всей длине балки. Пусть до деформации брус имел прямолинейную форму (рис. 3). Мысленно проведя нормальные к оси бруса сечения AB и A'B', вырежем бесконечно малый элемент бруса ABA'B', длину которого обозначим через l ₀.

Ввиду малости последней можно считать, что в результате изгиба отрезки AA', BB', NN' и все отрезки параллельные им перейдут в дуги окружности с центром на некоторой оси O, перпендикулярной плоскости рисунка (см. рис. 3). Эта ось называется осью изгиба.Наружные волокна, лежащие выше линии NN', при изгибе удлиняются, волокна, лежащие ниже линии NN', - укорачиваются. Длина отрезка NN' остается неизменной. Линия NN' называется нейтральной линией.

Рис.3

Проходящее через нее сечение (недеформированного) бруса плоскостью, перпендикулярной плоскости рисунка, называется нейтральным сечением. Пусть R - радиус кривизны нейтрального сечения (R = | NO |). Тогда l ₀=a R. Рассмотрим волокно бруса, находящееся на расстоянии x от нейтрального сечения. (x>0, если волокно выше нейтрального слоя, x<0, если - ниже.) Пусть брус не слишком толст, так что x<< R. Тогда длина рассматриваемого волокна равна l = a(R +x), а его удлинение D l = l - l ₀ = xa. Такое удлинение сообщается нормальной к AB силой, величина которой в расчете на единицу площади сечения AB равна:

. (11)

Будем считать, что мы имеем дело только с деформацией изгиба, т.е. сумма сжимающих и растягивающих сил, приложенных сечению AB равна нулю: , где dS - элемент площади рассматриваемого поперечного сечения бруса, интегрирование ведется по всему этому сечению. С учетом выражения (11) 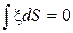. Отсюда ясно, что нейтральная линия и нейтральное сечение проходят через центр тяжести поперечного сечения бруса (например, AB). Из следует, что момент сил M _s,действующих на сечение AB, не зависит от того, относительно какой оси он берется. Для вычисления M _s проще всего взять ось, перпендикулярную плоскости рисунка и проходящую через точку N.

Очевидно, , (12)

или , (13)

где введено обозначение

. (14)

Величина I называется моментом инерции поперечного сечения бруса по аналогии с соответствующей величиной, вводимой при рассмотрении вращения тела вокруг неподвижной оси. Однако в отличие от последней величины, имеющей размерность массы, умноженной на квадрат длины, I, определяемый выражением (14), имеет размерность четвертой степени длины.

Для бруса с поперечным сечением в виде прямоугольника с шириной a и высотой (AB) b легко получить

. (15)

Направим ось X вдоль нейтральной линии недеформированного бруса, ось Y - перпендикулярно X в плоскости изгиба. Тогда уравнение нейтральной линии изогнутого бруса можно представить в виде y = y (x). По известной из математического анализа формуле

.

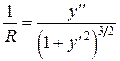Если изгиб мал (y '<<1), то квадратом производной можно пренебречь.

Тогда M_s = EIy". (16)

Рассмотрим теперь балку, лежащую на двух опорах (см. рис. 4). Расстояние между опорами равно L. Пусть на балку действует вертикальная сила F. Вследствие симметрии сила F равномерно распределится между опорами. Расстояние между точками О и О' (положениями центра масс до и после изгиба) называется стрелой прогиба. Обозначим ее через z. Поместим начало координат в точку A, направим ось X вправо, а Y - вниз. Отсечем мысленно часть балки, проведя нормальное сечение через произвольную точку С (x) (с координатой x < L /2). Справа на отсеченную часть балки будет действовать сила F /2, направленная вниз. Момент внешних сил, действующих на отсеченную часть, будет M = (F /2) x. Условие равновесия моментов принимает вид

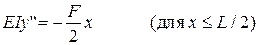. (17)

Знак минус в правой части обусловлен выбором системы координат: функция y (x), описывающая положение нейтральной линии, замедленно растет при x < L /2. Интегрируя уравнение (17) с учетом того, что y '(L /2) = 0 и y (0) = 0, найдем

. (18)

Тогда с учетом (15) получим стрелу прогиба для балки прямоугольного сечения

. (19)

Из выражения (19) легко получить рабочую формулу:

, (20)

где m  масса гири, g  ускорение свободного падения.

Дата добавления: 2015-06-26