Согласованный фильтр

Согласованный фильтр, или фильтр обнаружения, строится на основе критерия максимума пикового отношения сигнал/помеха на выходе фильтра и предназначен для решения задачи обнаружения сигнала. Под обнаружением сигнала понимается установление лишь факта наличия сигнала, достигаемое, в частности, за счет существенного искажения формы сигнала. Заметим, что выделение сигнала предусматривает оценку формы сигнала. Для согласованного фильтра обычно это невозможно. В то же время обнаружение сигнала обеспечивается для слабых сигналов с отношениями сигнал/помеха ниже уровня интенсивности помех.

Математической моделью для согласованного фильтра является аддитивная модель поля , для которой предполагается знание формы сигнала, а не его АКФ, как для фильтра Колмогорова-Винера.

Помеха задается в виде стационарного случайного процесса с известной АКФ, определяемой на участках с отсутствием полезных сигналов. Выбор формы сигнала (аномалии) осуществляется либо путем решения прямой задачи для конкретного геофизического метода, либо посредством анализа наблюденных значений над аномалиеобразующими объектами, где форма сигналов фиксируется визуально. При обработке временных разрезов в сейсморазведке оценка формы сигнала реализуется по значениям ВКФ соседних трасс или трасс, расположенных через некоторое удаление друг от друга, с таким расчетом, чтобы нерегулярные волны-помехи были бы некоррелированы.

Значение задачи обнаружения слабых сигналов непрерывно возрастает в связи с поисками глубокозалегающих и слабоконтрастных объектов, эффекты от которых искажены помехами разной природы, а интенсивность помех превосходит амплитуду полезных сигналов.

Критерий максимума пикового отношения сигнал/помеха сводится к максимизации следующего выражения

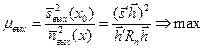(7.13)

Под пиковым отношением сигнал/помеха понимается отношение в одной, центральной точке 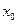выходного сигнала, для которого дисперсия 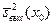равна квадрату скалярного произведения значений сигнала и весовой функции 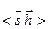, являющегося результатом свертки сигнала и весовой функции для точки .

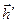Энергия (дисперсия) помехи на выходе фильтра равна квадратичной форме , где и 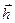- соответственно вектор-строка и вектор-столбец значений весовой функции, 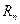- корреляционная матрица помехи, построенная для заданной АКФ помехи.

С целью максимизации (7.13) следует взять производную и ее приравнять к нулю, что обеспечивает получение системы линейных уравнений для нахождения весовой функции согласованного фильтра в матричной форме 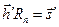(7.14) или в форме:

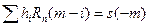(7.15)

Знак минус для абсциссы сигнала 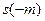означает, что значения сигнала отсчитываются с его конца, поскольку при свертке следует перевернуть либо весовую функцию, либо сигнал.

Применяя свойства преобразований Фурье к (7.15), получаем выражение для частотной характеристики согласованного фильтра 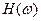: 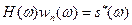, где 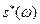- комплексно-сопряженный спектр сигнала, соответствующий «перевернутому» сигналу, т.е. сигналу, зеркально отражающему относительно оси ординат. Из последнего выражения следует, что

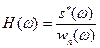(7.16).

Из (7.16) легко понять, почему фильтр получил название согласованный. Если помеху принять некоррелированной, то ее спектр определяется лишь значением дисперсии, т.е. , и 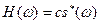. Иначе частотная характеристика фильтра согласована со спектром входного сигнала. Обратное преобразование Фурье при этом позволяет найти, что 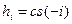, т.е. весовая функция согласована с формой сигнала. Иначе значения весовой функции полностью определяются значениями заданного по форме сигнала, а знак «минус» подчеркивает необходимость использования при свертке перевернутых его значений.

Пример 2. Пусть сигнал и помеха, как в примере 1, заданы значениями 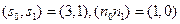, т.е.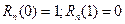

В соответствии с уравнением фильтра (7.15) имеем: или

.

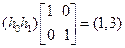Отсюда 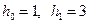. С учетом нормировки весовой функции .

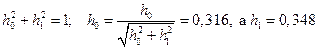Найдем пиковое отношение сигнал/помеха на выходе фильтра

,

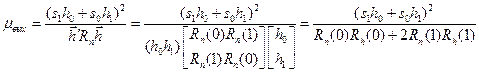где .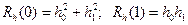

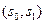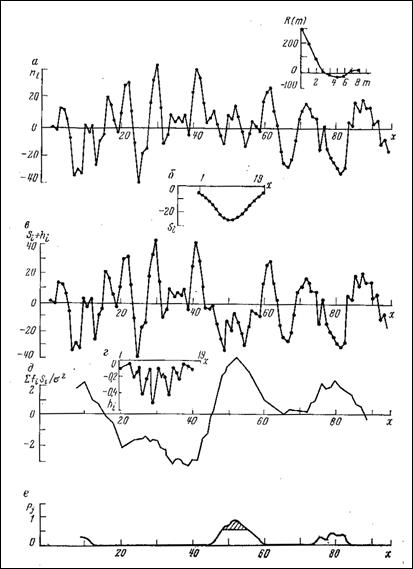
Подставляя в последнее выражение значения и найденные весовые коэффициенты, получаем 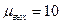. На рис.7.1 приведен пример иллюстрирующий результаты согласованной фильтрации.

 

Рис.7.1.Пример согласованной фильтрации. а – помеха и ее корреляционная функция R(m), б – полезный сигнал, в - сигнал плюс помеха, г - весовая функция согласованного фильтра, д - результат согласованной фильтрации, е - апостериорная вероятность наличия сигнала.

Дата добавления: 2015-06-26