Математический анализ опытных данных

За последние годы биологические науки, включая и зоотехнические, достигли значительных успехов. И немалая заслуга в том принадлежит математике. Немецкий философ Иммануил Кант писал: «Я утверждаю, что во всяком естественнонаучном знании можно найти лишь столько действительной науки, сколько в ней можно найти математики».

Широкое внедрение математических методов в биологию началось с конца 19-го века, когда английский ученый Фрэнсис Гальтон в 1899 году разработал основы новой науки, названной им биометрией (от греч. bios – жизнь, metreo – измеряю) – науки об использовании математических методов для изучения живых существ.

Задача биометрии – планирование биологических экспериментов и обработка результатов методами математической статистики. Необходимость использования математического анализа в биологии была связана с переходом от описательных методов к экспериментальным. А эксперимент (опыт) требует количественной оценки результатов, доказательства их достоверности.

Основные цели математического анализа опытных данных: выразить в сжатой, лаконичной форме накопленный цифровой материал, провести оценку достоверности полученных результатов исследований, сделать объективные выводы из проделанной работы.

Объектом математического анализа является изменяющийся (варьирующий) признак, то есть тот показатель, который изменяется под действием изучаемого в опыте фактора. Самым главным из этих признаков является продуктивность животных.

С помощью математического анализа в опытной работе решают следующие основные задачи:

1. определяют объем опыта, то есть устанавливают оптимальную численность животных в подопытных группах.

2. определяют средние значения изучаемых признаков с помощью средней арифметической, средней взвешенной, средней гармонической и др.

3. устанавливают степень изменчивости изучаемых признаков с помощью лимитов, среднего квадратического отклонения, коэффициента вариации, нормированного отклонения.

4. определяют достоверность полученных данных с помощью критерия достоверности.

5. определяют долю влияния изучаемых факторов на изменчивость признака путем дисперсионного анализа.

6. устанавливают направления и степень связи между признаками с помощью коэффициентов корреляции и регрессии.

Однако надо иметь в виду, что математические методы имеют в опытной работе вспомогательное значение. Они лишь помогают выявить то, что содержится в эксперименте. Никакая математическая обработка не поможет, если допущены методические просчеты в постановке опытов. Главными для исследователя являются биологические методы, вскрывающие суть жизненных процессов. Не случайно Д.И. Менделеев весьма скептически относился к так называемым математическим методам исследования, когда математикам кажется, что они способны решить любые задачи, тогда как на деле они не могут поставить эксперимент в подтверждение или опровержение своей теории.

Определение средних значений изучаемого признака. Как уже отмечалось, зоотехнические опыты являются сравнительными. В них сравнивают между собой группы и периоды, то есть средние величины изучаемых признаков. В зависимости от цели исследования определяют несколько средних величин: среднюю арифметическую, взвешенную среднюю арифметическую, среднюю гармоническую и др.

Средняя арифметическая – наиболее характерное значение признака для данной совокупности (группы), ее математический центр тяжести.

Среднюю арифметическую определяют по формуле:

где 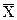– средняя арифметическая, ранее обозначали буквой М;

– значения признака для каждого члена совокупности (варианты), ранее обозначали буквой V;

n – общее число членов совокупности (группы)

(сигма – греческая прописная буква) – знак суммирования.

Например, в группе из 5 коров среднесуточный удой отдельных животных составил, кг: 10,5; 9,7; 13,5; 14,0; 12,3.

Чтобы вычислить среднюю арифметическую для этой группы, подставим данные в вышеприведенную формулу:

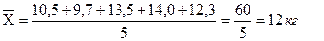
Для больших выборок, когда число особей более 30, раньше применяли непрямой способ вычисления средней арифметической. Для этого предварительно строили вариационные ряды. При использовании компьютеров необходимость в этом отпала.

Основные свойства средней арифметической:

· она характеризует совокупность (группу) в целом, а не отдельных ее членов;

· средняя арифметическая величина абстрактная, то есть может не совпадать ни с одной вариантой и иметь дробную величину. Например, в группе на свиноматку за год получено 1,7 опороса. Но ведь от каждой свиноматки можно получить или один, или два опороса за год;

· среднюю арифметическую применяют для характеристики однородной совокупности. Например, среднюю живую массу определяют по отдельным половозрастным группам.

Взвешенная средняя арифметическая определяется, когда разный математический вес признака. Например, требуется определить среднее содержание переваримого протеина в 1 кг смеси, состоящей из 70 кг ячменя и 30 кг гороха, если в 1 кг ячменя содержится 75 г переваримого протеина, а в 1 кг гороха – 210 г.

Взвешенную среднюю рассчитывают по формуле:

где – значение признака (варианта);

– математический вес признака.

Чтобы рассчитать взвешенную среднюю арифметическую, каждое значение признака умножают на его вес, все эти произведения суммируют и полученный результат делят на сумму весов.

Взвешенную среднюю применяют в зоотехнии часто, например, при определении процента жира молока за лактацию.

Средняя гармоническая (Н) – применяется для вычисления среднего уровня признака, характеризующего скорость какого-либо процесса (средняя скорость молокоотдачи, скорость бега, скорость яйцеобразования). Например, требуется определить среднюю скорость молокоотдачи у коровы, если за 4 минуты выдоено 8 кг молока, в том числе: за первую минуту – 2 кг, за вторую – 3, за третью – 2 и за четвертую – 1 кг. Для вычисления используют формулу:

При вычислении обычной средней арифметической скорость молокоотдачи составит 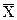= (2+3+2+1):4 = 2 кг. Как видим, фактический показатель меньше.

Показатели изменчивости. Средняя арифметическая – основной математический показатель, по которому судят о полученных результатах исследований. Однако средняя арифметическая не отражает изменчивость признаков, тогда как животные – объект зоотехнических исследований обладают большой изменчивостью признаков, особенно количественных. Это связано с многообразием внешних факторов, действующих на организм, а также с генетической особенностью каждой особи.

Основными показателями изменчивости (вариации) являются лимиты, среднее квадратическое отклонение, коэффициент вариации, нормированное отклонение.

Лимит (lim = х_max – х_min) – это разница между максимальным и минимальным значением признака в выборочной совокупности. Это наиболее простой показатель изменчивости признака. Чем больше величина лимита, тем значительнее изменчивость признака.

Среднее квадратическое отклонение (δ – сигма) основной показатель изменчивости. Его определяют по формуле:

В знаменателе данной формулы разница n-1 – это число степеней свободы, или число элементов свободного разнообразия. Так, если потребуется составить сумму из трех чисел, равную 100, то первые два числа могут быть любыми. Например, 50 и 30 или 500 и 300, а третье число должно быть одно: в первом случае – 20; (50 + 30 + 20 = 100), во втором – минус 700; (500 + 300 + (-700) = 100. При вычислении сигмы имеется одно ограничение. Оно определяется для группы, имеющей определенную среднюю арифметическую. Наличие в формуле знаков «+» и «-» указывает на то, что этот показатель характеризует изменчивость признака как в сторону увеличения от средней арифметической, так и в сторону уменьшения. Приведем пример расчета по количеству поросят в помете 5 свиноматок. Для этого удобнее пользоваться таблицей. В первую графу таблицы записывают варианты (в данном примере численность пометов), во вторую – отклонение каждой варианты от средней арифметической , в третью – квадраты отклонений .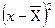

Дата добавления: 2015-06-26