Двухосный изгиб

(1) Общий метод, описанный в 5.8.6, может быть также использован для двухосного изгиба. Следующие правила действительны, когда применяются упрощенные методы. Особое внимание необходимо уделить нахождению сечения элемента с критической комбинацией моментов.

(2) В качестве первого шага необходимо произвести раздельный расчет в направлениях обеих главных осей, без учета двухосного изгиба. Несовершенства необходимо учитывать только в направлении, в котором они больше всего приводят к самым неблагоприятным воздействиям.

(3) Не требуется никакой дальнейшей проверки, если для гибкости выполняются следующие условия:

и (5.38а)

и если относительный эксцентриситет e_y / h и e _z/ b (рисунок 5.8), удовлетворяет одному из условий:

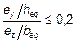или (5.38b)

где b, h — ширина и высота сечения;

и

— для эквивалентного прямоугольного сечения,

здесь i_y, i_z — радиусы инерции соответственно относительно оси y и оси z;

l _у, l _z — гибкость l ₀/ i соответственно относительно оси y и оси z;

— эксцентриситет нагрузки в направлении оси z;

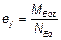— эксцентриситет нагрузки в направлении оси у,

здесь M_Edy — расчетное значение момента относительно оси y, включая моменты с учетом эффекта второго порядка;

M_Edz — расчетное значение момента относительно оси z, включая моменты с учетом эффекта второго порядка;

N_Ed — расчетное значение продольного усилия для соответствующего сочетания нагрузок.

Рисунок 5.8 — Определение эксцентриситетов e_y и e_z

(4) Если не выполняются условия (5.38), то необходимо учитывать двухосный изгиб, включая влияние эффектов второго порядка в обоих направлениях (если ими нельзя пренебречь согласно 5.8.2 (6) или 5.8.3). При отсутствии более точного расчета сечений при двухосном изгибе может быть использован следующий упрощенный критерий:

(5.39)

где M_{Edz / y} — расчетный момент относительно соответствующей оси, включая момент от эффектов второго порядка;

M_{Rdz / y} — предельный момент в соответствующем направлении;

a — показатель степени:

для круглых и эллиптических сечений а = 2;

для прямоугольных сечений:	NEd / NRd	0,1	0,7	1,0
a	1,0	1,5	2,0

для промежуточных значений допускается линейная интерполяция,

здесь N_Ed — расчетное значение продольной силы;

N_Rd = A_cf_cd + A_sf_yd — расчетное значение сопротивления сечения продольной силе,

A_c — площадь брутто бетонного сечения;

A_s — площадь продольной арматуры.

Дата добавления: 2015-06-26