Номинальная жесткость

Общие положения

Метод, основанный на номинальной жесткости

(1) В методе расчета с учетом эффектов второго порядка на основе жесткости, как правило, используются номинальные значения изгибной жесткости, которые рассчитываются с учетом влияния на общее поведение трещин, нелинейных свойств материалов и ползучести. Это применимо также и к соседним (смежным) элементам, которые учитывают при расчете, например, балки, плиты или фундаменты. При необходимости, следует также учесть взаимодействие «грунтовое основание — конструкция».

(2) Полученный расчетный момент используется для расчета поперечных сечений при действии изгиба с продольной силой согласно 6.1, с учетом 5.8.5 (1).

(1) Следующие модели применяются для определения номинальной жесткости гибких сжатых элементов с различными поперечными сечениями.

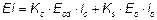, (5.21)

где E_cd — расчетное значение модуля упругости бетона, см. 5.8.6 (3);

I_c —момент инерции поперечного сечения бетона;

E_s —расчетное значение модуля упругости арматуры, см. 5.8.6 (3);

I_s —момент инерции арматуры относительно центра тяжести поперечного сечения бетона;

K_c —коэффициент, учитывающий влияние трещин, ползучести и т. п., см. 5.8.7.2 (2) или (3);

K_s —коэффициент, учитывающий влияние арматуры, см. 5.8.7.2 (2) или (3).

(2) В формуле (5.21) необходимо использовать следующие коэффициенты, с учетом, что r ³0,002:

r—геометрический коэффициент армирования, r = A_s / A_c,

где A_s —общая площадь поперечного сечения арматуры;

A_c —общая площадь поперечного сечения бетона;

j_ef —эффективный коэффициент ползучести, см. 5.8.4;

k ₁ —коэффициент, который зависит от класса прочности бетона, см. формулу (5.22);

k ₂ —коэффициент, который зависит от продольного усилия и гибкости, см. формулу (5.23):

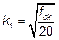, МПа, (5.22)

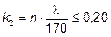, (5.23)

где n —относительное продольное усилие, n = ;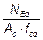

l—гибкость, см. 5.8.3.

Если не определена гибкость l, для k ₂может быть принято:

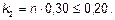(5.24)

(3) Как упрощенная альтернатива при r ³0,01 в формуле (5.21) могут быть использованы следующие коэффициенты:

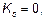(5.25)

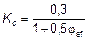. (5.26)

Примечание — Упрощенная альтернатива может использоваться в качестве первого шага, за которым следует более точный расчет согласно (2).

(4) В статически неопределимых конструкциях необходимо учитывать неблагоприятное влияние образования трещин в примыкающих элементах. Формулы (5.21) – (5.26) в общем случае не распространяются на такие элементы. При расчете может учитываться частичное образование трещин
и эффект ужесточения при растяжении, например, по 7.4.3. Для упрощения могут быть рассмотрены поперечные сечения, полностью пересеченные трещиной. Жесткость, как правило, следует рассчитывать с использованием эффективного модуля бетона.

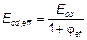, (5.27)

где E_cd — расчетное значение модуля упругости согласно 5.8.6 (3);

j_еf — эффективный коэффициент ползучести; допускается применять то же значение, что
и для колонн.

Дата добавления: 2015-06-26