Общий метод

Методы расчета

(1) Методы расчета включают общий метод, основанный на нелинейном расчете с учетом эффектов второго порядка (см. 5.8.6) и следующих двух упрощенных методов.

(а) Метод, основанный на номинальной жесткости, см. 5.8.7.

(b) Метод, основанный на номинальной кривизне, см. 5.8.8.

Примечание 1 — Выбор упрощенного метода ((a) и (b)) для применения в своей стране может быть указан
в национальном приложении.

Примечание 2 — Номинальные моменты, определенные с учетом эффектов второго порядка с помощью упрощенных методов (a) и (b) иногда могут быть больше, чем соответствующие потере устойчивости. Тем самым необходимо убедиться, что общий момент совместим с сопротивлением поперечного сечения.

(2) Метод (a) может применяться как для отдельных элементов, так и для конструкции в целом, если значения номинальной жесткости рассчитаны предварительно, см. 5.8.7.

(3) Метод (b) подходит преимущественно для отдельных элементов, см. 5.8.8. При реальных предпосылках в части распределения кривизны метод по 5.8.8 может быть применен для конструкций.

(1)P Общий метод основан на нелинейном расчете, включающем геометрическую нелинейность, т. е. эффекты второго порядка. Применяются общие правила для нелинейного расчета по 5.7.

(2)Р Следует использовать зависимости напряжений от относительных деформаций для бетона и стали, пригодные для общего расчета. Необходимо учитывать влияние ползучести.

(3) Могут быть использованы зависимости «напряжение — относительная деформация» для бетона и стали, которые приведены в 3.1.5, уравнении (3.14) и 3.2.7 (см. рисунок 3.8). По определенным на основе
расчетных значений диаграммам «напряжение — относительная деформация» напрямую из расчета определяется расчетное значение предельной нагрузки. В уравнении (3.14) и в выражении для определения значения k значение f_cm заменяется расчетным значением прочности бетона f_cd, а E_cm заменяется

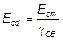. (5.20)

Примечание — Значение g _СE может быть приведено в национальном приложении. Рекомендуемое значение равно 1,2.

(4) При отсутствии более точных моделей ползучесть может быть учтена умножением всех значений относительных деформаций диаграммы «напряжение — относительная деформация» для бетона согласно 5.8.6 (3) на коэффициент (1 + j_ef), где j_ef является эффективным коэффициентом ползу­чести согласно 5.8.4.

(5) Может быть учтен благоприятный эффект ужесточения при растяжении.

Примечание — Этот эффект является благоприятным и для упрощения расчетов в каждом случае может
не учитываться.

(6) Обычно условия равновесия и совместности деформаций проверяются в нескольких поперечных сечениях. Упрощенной альтернативой является рассмотрение только критических сечений
и принятие подходящего изменения кривизны между ними, например, подобно изгибающему моменту с учетом эффектов первого порядка или в соответствии с другим приемлемым способом.

Дата добавления: 2015-06-26