
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел последовательности комплексных чисел
|
|
|
|
Лекция №3
Степень с произвольным рациональным показателем
Пример.
Вычислим корень из (-1).
 , очевидно |-1| = 1, arg (-1) = π
, очевидно |-1| = 1, arg (-1) = π
-1 = 1·(cos π +i·sin π)
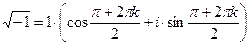 , (k = 0, 1).
, (k = 0, 1).
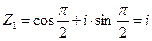
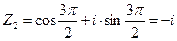
 =
= 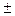 i
i
Возьмем произвольное комплексное число с. Если n натуральное число, то сn = |c|n·(сos nArg с + i·sin nArg с) (6). Эта формула верна и в случае n = 0 (с≠0) 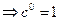 . Пусть n < 0 и n
. Пусть n < 0 и n 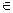 Z и с ≠ 0, тогда
Z и с ≠ 0, тогда
сn = 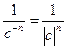 (cos nArg с+i·sin nArg с) =
(cos nArg с+i·sin nArg с) = 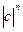 (cos nArg с + i·sin nArg с). Таким образом, формула (6) справедлива для любых n.
(cos nArg с + i·sin nArg с). Таким образом, формула (6) справедлива для любых n.
Возьмем рациональное число 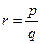 , где q натуральное число, а р является целым.
, где q натуральное число, а р является целым.
Тогда под степенью cr будем понимать число 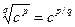 .
.
Мы получаем, что 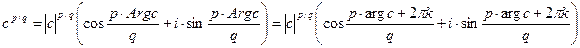 ,
,
(k = 0, 1, …, q-1). Этих значений q штук, если дробь не сократима.
Комплексно-значная функция натурального аргумента называются последовательностью комплексных чисел и обозначается (сn) или с1, с2,..., сn. сn = аn+bn·i (n = 1,2,...) комплексные числа.
с1, с2, … - члены последовательности; сn – общий член
Комплексное число с = a+b·i называется пределом последовательности комплексных чисел (cn), где сn = аn+bn·i (n = 1, 2, …), где для любого 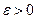
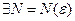 , что при всех n > N выполняется неравенство
, что при всех n > N выполняется неравенство 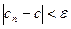 . Последовательность, имеющая конечный предел называется сходящейся последовательностью.
. Последовательность, имеющая конечный предел называется сходящейся последовательностью.
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 562; Нарушение авторских прав?; Мы поможем в написании вашей работы!