Основные понятия многочленов

Пример.

Признак Даламбера.

Признак Коши.

Пусть для ряда (1) существует предел 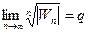, тогда если q < 1, то ряд (1) абсолютно сходится, если q>1, то ряд (1) расходится.

Если для ряда (1) комплексных чисел существует предел 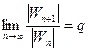, то при q < 1 этот ряд абсолютно сходится, а если q > 1, то ряд расходится.

Исследовать на абсолютную сходимость ряд 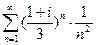, здесь .

Найдем 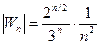. Очевидно 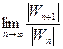= = 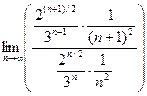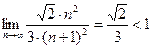. Следовательно, ряд абсолютно сходится.

Абсолютно сходящиеся ряды можно перемножать. Произведение абсолютно сходящегося на сходящийся ряд – сходится. Произведение двух сходящихся может расходиться.

Пусть Е некоторое множество точек комплексной плоскости (Z). Точка Z_0, принадлежащая (Z), называется предельной точкой из множества E, если в любой ее ε- окрестности (O_ε (Z₀): |Z – Z₀| < ε) содержится бесконечное число точек из множества Е.

Множество 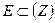называется замкнутым, если любая точка Z, не принадлежащая Е, не является предельной для Е, иначе говоря, если Е содержит все свои предельные точки, если они существуют. В конечном множестве предельных точек нет, но оно замкнуто.

Множество 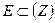называется ограниченным, если оно содержится в некотором круге. Это определение эквивалентно следующему: множество E называется ограниченным, если существует число М > 0, что для любого Z принадлежащего E выполняется неравенство 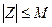, т. е. если оно содержится в некотором круге началом в точке нуль.

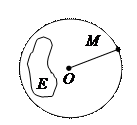
Расстояние между точкой Z₀, принадлежащей (Z), и множеством 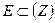, называется нижней гранью расстояний от точек Z₀ до всевозможных точек множества Е.

ρ(Z₀, Е) =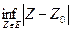

Если Z₀ не принадлежит Е, а расстояние от Z₀ до Е равно 0 (ρ(Z₀, Е) =0), то Z₀ является предельной точкой множества Е. Следовательно, если множество Е замкнуто, а Z₀ не принадлежит Е, ρ(Z₀, Е) > 0, в противном случае, Z₀ была бы предельной точкой множества Е.

Расстояние между множествам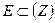и и 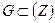называется нижней гранью расстояний (всевозможных) то точек множества E до точек множества G. .

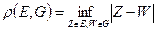Легко доказывается, что если множества E, G замкнуты, 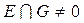и, по крайней мере, одно из них ограничено, то ρ(E,G) > 0.

Как мы знаем, всякое бесконечное ограниченное множество 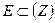имеет, по крайней мере, одну предельную точку. Рассмотрим теперь произвольное неограниченное множество 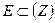. Может случится, что в некотором круге содержится бесконечное число точек из E, тогда в нем будет содержаться предельная точка множества Е.

Пусть в любом таком круге содержится лишь конечное число точек из множества E, тогда в его внешности будет содержаться бесконечное число точек из множества E. следовательно в ρ -окрестности бесконечно удаленной точки будет содержаться бесконечное число точек из множества E, поэтому бесконечность в этом случае будет предельной точкой для множества Е. Таким образом, всякое бесконечное множество точек комплексной плоскости имеет по крайней мере одну предельную точку, конечную или бесконечную.

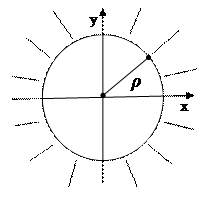
Пусть E некоторое множество плоскости (Z) (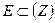), а {K} множество открытых кругов плоскости. Будем говорить, что система кругов {K} покрывает множество E, если любая точка Z, принадлежащая E, содержится, по крайней мере, в одном из кругов K, системы {K}. Справедлива теорема Бореля – Лебега о покрытии.

Дата добавления: 2015-06-26