Непрерывные кривые

Понятие обобщенно непрерывной функции

Теорема.

Всякая непрерывная на замкнутом ограниченном множестве E плоскости (Z) функция f(Z) равномерно непрерывна на этом множестве.

Отметим, что непрерывная на замкнутом ограниченном множестве 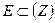функция f(Z₀) является ограниченной, т. е. существует М > 0, такая, что для любой Z принадлежащей E выполняется неравенство .

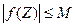Будем теперь предполагать, что функция в некоторых точках может обращаться в бесконечность. Пусть, например f(Z₀) = ∞, где Z₀ предельная точка множества E, на котором задана f(Z₀).

Если 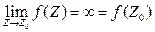, то функция f(Z) называется обобщенно непрерывной в точке Z₀.

Понятие непрерывной кривой обобщает понятие траектории движущейся точки.

Пусть на некотором отрезке [ α,β ] задана непрерывная комплексно-значная функция вещественной переменной Z = Z(t) = x(t)+i·y(t) (t принадлежит [ α,β ]). Будем истолковывать переменную t как время, а значение Z(t) как точку комплексной плоскости. Тогда с изменением времени t от α до β точка Z(t), перемещаясь в комплексной плоскости (Z) опишет некоторую траекторию. Эта траектория и будет непрерывной кривой.

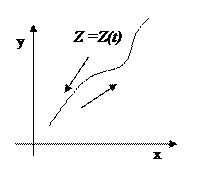
Если задана непрерывная комплексно-значная функция вещественной переменной t (Z = Z(t)) на некотором отрезке [ α,β ], то говорят, что эта функция определяет в плоскости (Z) непрерывную кривую.

На кривой (Z = Z(t)) можно выбрать два направления. Одно из них соответствует возрастанию t от α до β, а второе убыванию t от β до α.

Точка Z кривой (Z = Z(t)) (t принадлежит [ α,β ]) называется кратной точкой, если она соответствует не одному, а нескольким значениям параметра t принадлежащего [ α,β ], одно из которых (по крайней мере) отличается как от α, так и от β.

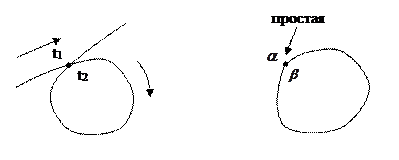
Все точки кривой не являющиеся кратными называются простыми точками кривой.

Кривая, состоящая из одних простых точек, называется простой кривой или кривой Жордана.

Кривая называется замкнутой, если начало и конец ее совпадают, т. е. если Z(α) = Z(β).

Будем считать, что две непрерывные функции Z = λ(t) 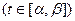и 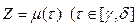) определяют одну и ту же непрерывную кривую в плоскости (Z), если существует такая монотонная непрерывная функция 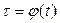, отображающая отрезок [ α,β ] на [ γ,δ ], что для любого t принадлежащего [ α,β ], выполняется равенство λ(t) = μ [ φ(t) ].

Функция Z = cost, t принадлежит [ 0,π ] определяет непрерывную кривую, совпадающую с отрезком [ -1,1 ].

Рассмотрим теперь кривую Z = cos2t, t принадлежит [ 0,π ], эта кривая геометрически так же совпадает с отрезком [ -1,1 ], однако эта кривая отличается от первой, т. к. она замкнута и состоит из кратных точек, за исключением точки -1, 1. Справедлива теорема Жордана.

Дата добавления: 2015-06-26