Пример (дробно-линейная функция)

Геометрический смысл модуля производной

Лекция №10

Из определения производной , следовательно, 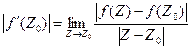(1).

Очевидно, 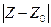– это есть расстояние между точками Z и Z₀, или что тоже – длина вектор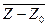а . А – это есть расстояние между их образами f(Z) и f(Z₀) или длина вектора f(Z) – f(Z₀). Значит, отношение 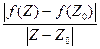можно рассматривать как растяжение вектора с началом в точке Z₀ и концом в точке Z при отображении W = f(Z).

Поэтому, в силу равенства (1), модуль производной 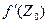можно рассматривать как растяжение в точке 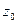при отображении W = f(Z). Очевидно, это растяжение, вообще говоря, не совпадает с отношением 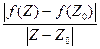, но является его пределом, и это растяжение не зависит от выбора точки .

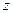Функция вида W = f(z) = 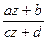(2) называется дробно-линейной функцией (здесь a, b, c, d – фиксированные комплексные числа, а z – комплексная переменная).

Мы будем рассматривать случай, когда (3).

Очевидно, в случае 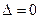строки определителя пропорциональны.

Пусть ,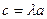

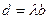
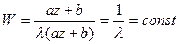и этот случай не интересен, так как вся плоскость переводится в одну точку.

Очевидно, выполняется, по крайней мере, одно из условий:

а) с = 0;

б) с ≠ 0.

а) Рассмотрим случай с = 0, так как 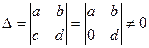, то обязательно a и d не равны нулю. Положим 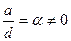, , 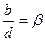тогда отображение (2) запишется в виде 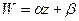, 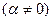(4).

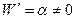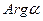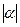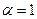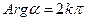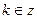Очевидно производная , поэтому отображение (4) конформно в любой точке плоскости (Z). При этом отображении угол поворота касательной к кривым постоянен во всех точках плоскости (Z) и равен . Растяжение также во всех точках будет фиксировано и будет равно . Очевидно, если , то , и .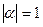

Следовательно, в этом случае отсутствует поворот и растяжение.

Отображение 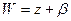осуществляет при этом сдвиг всей плоскости на вектор .

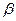Пусть теперь 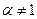. Тогда отображение (4) можно переписать так 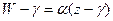, где 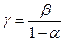. Отсюда видно, что 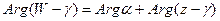и .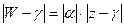

Таким образом, в данном случае при отображении (4) векторы 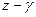, выходящие из точки 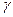, растягиваются в 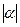раз и затем поворачиваются на угол 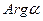. Следовательно, при этом отображении вся плоскость относительно точек 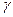растягивается в 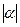раз и затем поворачивается на угол .

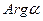б) Пусть теперь с 0. Очевидно, 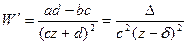, где 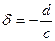, число 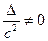. Нетрудно видеть, что производная конечна и отлична от нуля во всех точках 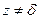, поэтому 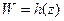является конформным во всех точках 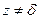. При этом отображении касательные к кривым поворачиваются на угол 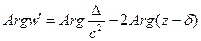. Растяжение во всех точках будет равно .

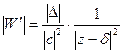Из этих формул непосредственно видно, что поворот касательных к кривым будет одним и тем же в тех точках 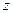, где 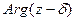сохраняет постоянное значение. Очевидно, это будут лучи 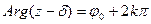, исходящие из точек 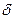. Растяжение будет одним и тем же только в точках 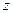, где 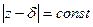, то есть на окружностях с центром в точке .

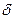Дата добавления: 2015-06-26