Замечания

1. Выражение exp( ∞ ) лишено смысла, т.к. 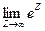не существует.

2. expZ не совпадает ни с одним многочленом, так как всякий многочлен не равный постоянной, стремится к бесконечности при Z → ∞

P_n = a₀+a₁Z+…+a_nZⁿ

Целые функции отличные от многочленов называются трансцендентными, следовательно, экспонента Z (expZ) есть трансцендентная целая функция.

Возьмем плоскость (Z) и систему координат

По первому свойству показательной функции, показательная функция нигде в нуль не обращается, т. е. W = 0 не принимает этой функции не при каком Z. Следовательно, образом плоскости Z при отображении W = e^Z является плоскость (W). Покажем, что всякая другая точка плоскости (W) является образом. Дано отображение: W = expZ, где Z = x+i·y.

По 1. , т. е. y = ArgW

Итак, прообразом точки W будет точка Z:

Покажем, что любая k из найденных Z является прообразом W. Итак,

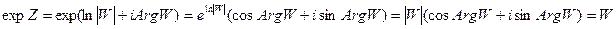
Итак, мы получим, что expZ = W, следовательно, каждая из найденных Z есть прообраз точек W.

Множество всех корней уравнения W = e^Z (W ≠ 0) представляется формулой:

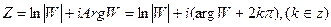(1)

Так как ArgW имеет бесконечное множество значений, различающихся попарно на целые ограниченные 2π, то точек Z бесконечно много. Следовательно, отображение W = expZ не взаимно однозначно, т. к. k -тая точка W ≠ 0 имеет бесконечное множество прообразов.

Так как производная показательной функции всюду отлична от нуля, то отображение W = e^Z конформное, то во всех точках плоскости (Z). Заставим Z описывать некоторую прямую, на пример, параллельную. Что является образом прямой параллельной мнимой оси при отображении W = e^Z?

Уравнение этой прямой Z = c+i·t, тогда

W = e^Z = e^c+it = e^c·(cost+isint),

таким образом, этой прямой будет окружность радиуса e^c c центром вначале координат. При этом, когда точка Z описывает прямую так что ордината этой точки равна t непрерывно растет от – ∞ до +∞, то W описывает соответствующую окружность бесконечно много раз в одном и том же направлении (положение против часовой стрелки).

Пусть теперь точка Z описывает прямую, параллельную действительной оси. Что является образом прямой параллельной действительной оси при отображении W = e^Z? Заменим уравнение этой прямой Z = t+i·c', тогда W=e^Z=e^t+i·c'=e^t·(cos c' +I sin c').

Итак, образом прямой, параллельной действительной, оси будет являться луч, выходящий из начала координат и образующий с положительной частью действительной оси и угол c'. При этом, когда Z описывает прямую так, что абсцисса этой точки равная t, непрерывно растет от - ∞ до + ∞, то и W описывает соответствующий луч так, что расположение этой точки от начала координат непрерывно растет от 0 до ∞ (0 исключается).

Теорема.

При отображении W = e^Z плоскости (Z) семейство прямых параллельных мнимой оси преобразуется в семейство окружностей с центром в начале координат, а семейство прямых параллельных действительной оси в – семейство прямолинейных лучей, выходящих из начала координат.

Рассмотрим область g, представляющую собой внутренность прямолинейной полосы, параллельной действительной оси, шириной h ().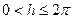

Что является образом этой полосы при отображении W = e^Z? Образом прямой y=φ₀ будет луч.

Итак, образом области g, входящей в (Z), будет область d, представляющая угол раствора h с вершиной в начале координат, ограниченной прямолинейными лучами.

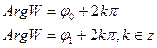
При этом соответствии между точками областей g и d, устанавливаемым функцией W = e^Z, отображение будет взаимно однозначным. Действительно, прообразом некоторой точки W 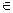d, могут быть только точки

,

различающиеся друг от друга значениями мнимой части. Две такие точки лежат на прямой параллельной мнимой оси на расстоянии кратном 2π, но наша полоса g имеет ширину не более 2π, поэтому она может содержать внутри лишь один прообраз точки W.

Итак, показательная функция W = e^Z, взаимно однозначно отображает полосу ширины 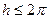, параллельную действительной оси на угол раствора h с вершиной в начале координат.

Дата добавления: 2015-06-26