Однозначные ветви многозначных функций

Лекция №19

Формулы приведения.

Из равенств

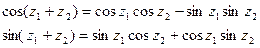
непосредственно вытекают формулы приведения, аналогичные функциям приведения для вещественных функций sinx и cosx.

Докажем, например, что справедливы равенства:

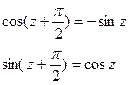
В самом деле, полагая, что Z₁ = Z, а Z₂ = мы получаем:

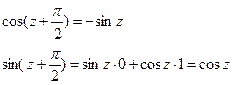
Аналогично выводятся остальные формулы приведения.

Пусть функция W = f(Z) отображает множество 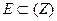, на множество 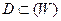, тогда функция Z = φ(W), отображающая множество D на множество E, которая ставит в соответстви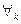е точке 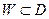ее полный прообраз при отображении W = f(Z), т. е. все такие 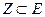, в которых f(Z) = W, называется обратной функцией.

Обратные функции комплексного переменного для однозначных функций W=f(Z), как правило, являются многозначными.

Например, для функции W = Zⁿ обратная функция является n -значной, а для функции W = e^Z обратная функция Z = lnW будет бесконечно-значной.

С целью изучения многозначной функции при помощи разработанного аппарата для однозначных функций выделяют однозначные ветви. Это осуществляется по следующей схеме:

Пусть в области g 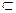(W) нам задана однозначная обобщенно непрерывная функция Z = f(W). Как известно, образ G 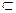(Z) области g будет также областью.

Пусть область g каким-то образом удалось разбить на конечное или счетное число попарно не пересекающихся областей g_k, обладающих свойствами:

1. 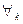точки (W) 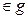либо принадлежащей только какой-то одной области g_k, либо являющейся граничной точкой нескольких областей g_k.

2. Функция Z = f(W) переводит две различные точки (W₁) и (W₂) 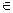g_k в различные точки, т. е. отображение является взаимно однозначным.

Легко видеть, что образами областей g_k 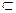(W) при отображении Z = f(W) будут и области G_k 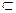(Z), причем граничные точки областей g_k, которые принадлежат g, будут отображаться в граничные точки областей G_k.

Легко видеть, что отображение Z = f(W) области g_k будет взаимнооднозначным. Поэтому существует однозначная обратная функция W=F_k(Z), отображающая уже G_k на g_k. При различных k мы получаем различные обратные функции.

Эти однозначные обратные функции и называются ветвями обратной функции W = F(Z), отображающей множество G на множество g.

Эти ветви получаются следующим образом из обратной функции W = F(Z). Значения функции W = F(Z) на G_k ограничиваются тем, что принадлежат области g_k.

Z=f(W) задана на g 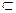(W), обратная функция W=F(Z) задана на множестве G=f(g) плоскости (Z) (это многозначная функция).

Область g разбили на части g₁, g₂, …,g_n, образы их будут областью G_k для 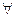g.

Существует функция W=F_k(Z), однозначная ветвь обратной функции W=F(Z), значение функции W=F(Z) ограничиваются тем…

Как видно, характер областей G_k 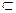(Z) и, следовательно, характер однозначных ветвей W = F_k(Z) существенно зависит от способа разбиения области g 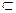(W) на области g_k.

Отметим, что в прошедших случаях удается разбить область g плоскости (W) на части g_k таким образом, что все их образы G_k будут совпадать между собой. Обозначим их через 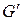. Тогда на одном и том же множестве 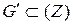определятся однозначные ветви W = F_k(Z).

Приведенный способ выделения однозначных ветвей из многозначной функции, вообще говоря, не применим к произвольным обобщенно непрерывным функциям Z = f(W), но он всегда применим к аналогичным функциям Z = f(W) в области g 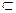(W), за исключением изолированных точек, в которых функция обращается в бесконечность.

Аналитическая функция Z = f(W) называется однолистной в области g 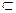(W), если она принимает различные значения в различных точках множества g, т.е. является инъективной.

Если же функция Z = f(W) принимает одно и тоже значения в некоторых точках области g 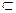(W), то она называется многолистной.

Выше мы разбиваем область g 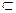(W) на области одномерности g_k, в которой она была однолистной. Таким образом, выделение однозначных ветвей многозначной функции сводится к разбиению многолистной области g 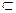(W) функции Z = f(W) на области однолистности g₁, g₂, …

Дата добавления: 2015-06-26