Понятие о подобии объектов

Подобие есть определенное отношение между значениями показателей свойств различных объектов, наблюдаемое и измеряемое исследователем в процессе познания. Под подобием понимается такое взаимно однозначное соответствие (отношение) между свойствами объектов, при котором существует функция или правило приведения значений показателей данных свойств одного объекта к значениям тех же показателей другого объекта.

Математические (формальные) описания подобных объектов допускают приведение их к тождественному виду.

Другими словами, подобие есть отношение взаимно однозначного соответствия между значениями показателей однородных свойств различных объектов. Однородными называются свойства, имеющие одинаковую размерность показателей.

Вообще говоря, объекты с различной физической природой, например механические и электрические процессы, могут иметь однородные свойства, например свойство изменения во времени определенных параметров.

Известно несколько видов подобия объектов [3].

1. В зависимости от полноты учета параметров различают:

абсолютное (теоретическое) подобие, которое предполагает пропорциональное соответствие значений всех параметров данных объектов,

т. е. p_j(t) / r_j(t) = m_j(t), где j=1,n;

практическое подобие - определенное функциональное взаимно однозначное соответствие параметров и показателей определенного подмножества свойств, существенных для данного исследования;

практическое полное подобие - соответствие показателей и параметров выделенных свойств во времени и пространстве;

практически не полное подобие - соответствие параметров и выделенных свойств показателей только во времени, или только в пространстве;

практическое приближенное подобие - соответствие выделенных параметров и показателей с определенными допущениями и приближениями.

2. По адекватности природы объектов различают:

физическое подобие, предполагающее адекватность физической природы объектов (частными случаями физического подобия являются механическое, электрическое и химическое подобия объектов);

математическое подобие, предполагающее адекватность формального описания свойств объектов (частными случаями математического подобия являются статистическое, алгоритмическое, структурное и графическое подобие показателей свойств объектов).

Проблема определения подобных объектов состоит в выборе научно обоснованных критериев подобия и в разработке методов расчета этих критериев.

Изучению проблемы подобия объектов посвящена теория подобия. В рамках этой теории установлены три основных теоремы о подобии объектов, определяющие необходимые и достаточные условия подобия (критерии подобия).

Приведем краткое изложение содержания этих теорем [3].

Теорема I. Подобные объекты имеют числено равные коэффициенты подобия (в теории подобия они называются критериями подобия), образованные из определенных сочетаний размерностей соответствующих параметров.

Чаще всего коэффициенты подобия представляют собой степенные комплексы размерностей, полученных из отношений (размерностей) параметров, учитываемых при описании объектов.

Например. Переходный процесс в электрическом контуре рис. 1.3.

может быть описан следующим дифференциальным уравнением:

du_с / dt + u_c - E = 0.

Рис. 1.3. Электрический контур с параметрами R, C, E, t, u_с.

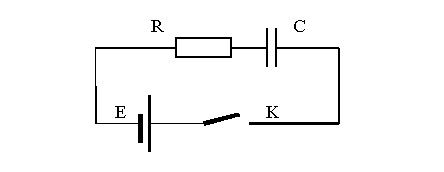
Параметрами этого процесса являются: R, C, E, u_с, t.. Из данного уравнения путем определенных преобразований получают следующие коэффициенты подобия:

p ₁ = RC/ t= R¹ C¹ t^-1 u_c⁰ E⁰,

p ₂ = E/u_c = E¹ u_c^-1 R⁰ C⁰ t⁰.

Коэффициенты подобия являются безразмерными величинами. Их значения одинаковы для любых наборов значений параметров электрического контура данного вида, т.е. для всех подобных электрических контуров с заданной схемой и номенклатурой параметров, взаимосвязанных приведенным выше дифференциальным уравнением.

Данная теорема носит имя Ньютона, или Ньютона-Бертрана.

Теорема II. Всякое уравнение физического процесса F(p₁,...,p_n)= 0, записанное в определенной системе единиц измерений, может быть представлено в виде соответствующего уравнения F^`(p ₁,..., p _m) = 0 между коэффициентами подобия p ₁,..., p _m, полученными из параметров p₁,...,p_n, задействованных в исходном уравнении F(p₁,...,p_n--k)= 0.

Для примера, показанного на pис.1.3., это уравнение имеет вид: 1+ p ₁ - p ₂ = 0.

Данная теорема называется p-теоремой. Она говорит о том, что множество описаний подобных объектов можно привести к единому уравнению соответствующих коэффициентов подобия. Все подобные объекты имеют единый математический образ.

Теорема III. Необходимыми и достаточными условиями подобия объектов (оригинала и модели), описываемых однородными уравнениями F(P₁,...,P_m)= 0 и F(R₁,...,R_m)= 0, являются:

1. пропорциональность значений параметров P_i / R_i = m_i,
2. равенство (m = k - 1) коэффициентов подобия, составленных из данных уравнений, где m - число всех параметров в уравнении, k - число независимых параметров в уравнении,
3. соблюдение однозначности начальных условий и не учитываемых, неизменяемых параметров, т.е. соблюдение однозначности условий эксперимента.

Известны также дополнительные условия подобия для сложных объектов [3]. Смысл этих дополнительных условий в следующем. Два сложных объекта подобны, если подобны все соответствующие элементы этих объектов и подобны функции (или отношения) связывающие данные элементы.

По мере развития науки о моделировании, подобие приобретает все более широкое содержание. Возникли особые виды подобия:

квазиподобие, основанное на использовании переменных масштабных коэффициентов;

эквивалентное подобие, основанное на сравнении эквивалентных в том или ином смысле описаний, например на взаимно однозначном соответствии функций на некотором интервале;

алгоритмическое подобие, основанное на сопоставлении выполняемых алгоритмов;

кибернетическое подобие, основанное на подобии функций управления, реализуемых различными объектами.

Далее мы будем говорить только о математическом подобии сложных процессов.

Дата добавления: 2015-06-04