Понятие о научном эксперименте, принцип максимального правдоподобия математических моделей

Выше было показано, что всякая математическая модель является только приближенным описанием некоторых свойств соответствующего реального объекта.

Единственным способом проверки степени соответствия модели и моделируемого объекта является научный эксперимент. Под экспериментом понимают целенаправленно организованный опыт, состоящий из воспроизведения и наблюдения исследуемого явления с необходимой точностью.

Математическое моделирование также представляет собой эксперимент, цель которого состоит в том, чтобы опытным путем, или путем логического вывода, найти неизвестные параметры q₁,..., q_m математической модели изучаемого процесса или объекта и построить соотношение Y^* = F^*(x₁,..., x_n, z₁,..., z_r, q₁,... q_m) в явном виде так, чтобы в области варьирования факторов x₁,..., x_n, z₁,..., z_r функция Y^* наилучшим образом приближалась бы к функции Y.

Достижение этой цели основано на использовании принципа максимального правдоподобия математической модели (функции F^*) экспериментально полученным данным об исследуемом объекте.

Принцип максимального правдоподобия основан на следующих известных положениях теории вероятностей.

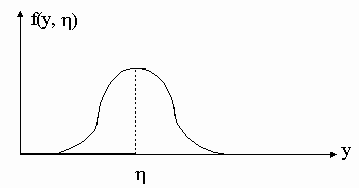
1. Случайная величина Y полностью определяется (задается) функцией плотности распределения f(y,h) ее значений, где h - параметр плотности распределения.

2. Математическое ожидание случайной величины Y есть наиболее вероятное (правдоподобное) ее значение. Оно вычисляется по формуле:

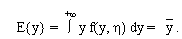
E{y} соответствует максимальному значению этой функции.

Другими словами, наиболее вероятное значение E{y} случайной величины Y соответствует значению параметра h функции f(y, h), удовлетворяющему условию:

d f(y,h)/ dh = 0, (1.5)

где h - среднее значение величины y.

Рис. 1.4. График функции плотности распределения вероятностей

Уравнение (1.5) называется уравнением правдоподобия, а решение h^ этого уравнения называется оценкой максимального правдоподобия случайной величины Y по параметру h. Оценка h^ параметра h осуществляется экспериментально по выборке значений y₁,..., y_n случайной величины Y из генеральной совокупности ее значений. При этом исходят из того, что вероятность получить выборку значений y₁,..., y_n определяется по формуле:

(1.6)

где - совместная плотность распределения выборки y₁,..., y_n

в генеральной совокупности значений случайной величины Y.

Из данного выражения следует, что наибольшему значению вероятности (1.6) соответствует максимальное значение функции

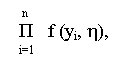(1.7)

вычисленное по параметру h.

Функция (1.7) называется функцией правдоподобия h (среднего значения случайной величины Y) и записывается в виде l{h / y₁,..., y_n}. Часто применяется также логарифмическая функция правдоподобия, которая позволяет упростить вычисление оценки h^ параметра h по выборке y₁,..., y_n.

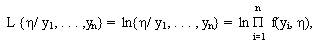(1.8)

Дата добавления: 2015-06-04