
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение плоской электромагнитной волны
|
|
|
|
Уравнениям Максвелла в интегральной форме, приведенным в § 20.2, с помощью известных теорем векторного анализа (теорем Стокса и Остроградского-Гаусса) можно придать дифференциальную форму (см. приложение 5):
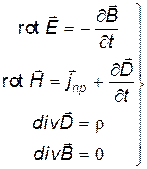
| (24.1) |
В координатной форме уравнения Максвелла (24.1) имеют вид
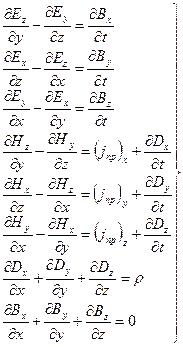
| (24.2) |
Рассмотрим случай неограниченной однородной среды, представляющей собой диэлектрик, в котором отсутствуют электрические заряды. Для такой среды 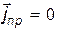 и r = 0. Кроме того, будем предполагать, что векторные характеристики электромагнитного поля
и r = 0. Кроме того, будем предполагать, что векторные характеристики электромагнитного поля  (и соответственно
(и соответственно 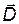 и
и  ) зависят только от координаты x. Тогда система уравнений (24.2) принимает вид
) зависят только от координаты x. Тогда система уравнений (24.2) принимает вид
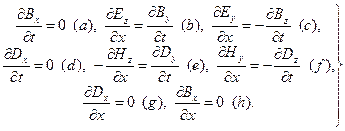
| (24.3) |
Из уравнений (a), (d), (g) и (h) следует, что x-компоненты электромагнитного поля Bx и Dt не зависят от x и t, т.е. Bx(x,t)=const, Dx(x,t)=const.
Оставшиеся четыре уравнения распадаются на две независимых системы уравнений. В одну из них входят y-компоненты электрического поля и z-компоненты магнитного поля, а в другую — z-составляющие электрического и y-составляющие магнитного поля:
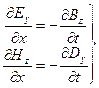
| (24.4) |
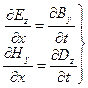
| (24.5) |
Эти системы уравнений однотипны, поэтому ограничимся рассмотрением одной из них — системы уравнений (24.4).
Учитывая, что D=e0eE, а B=m0mH, перепишем систему уравнений (24.4) в виде
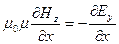 ; ;
| (24.6) |
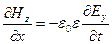 . .
| (24.7) |
Теперь, чтобы найти зависимость изменений электрического поля в пространстве от его же изменений во времени, продифференцируем (24.6) и (24.7) соответственно по координате и времени:
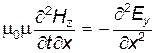 ; ;
| (24.8) |
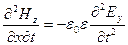 . .
| (24.9) |
Смешанные производные равны, т.е. 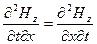 , поэтому из (24.8) и (24.9) легко получить
, поэтому из (24.8) и (24.9) легко получить
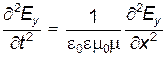 . .
| (24.10) |
Последнее уравнение и представляет собой уравнение плоской электромагнитной волны. Аналогичное уравнение можно получить и для магнитной составляющей
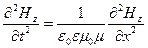 .
.
Сравнивая (24.10) с (22.5), можно установить, что скорость электромагнитной волны определяется выражением
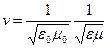 . .
| (24.11) |
Сомножитель 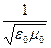 — это скорость распространения электромагнитных волн в вакууме:
— это скорость распространения электромагнитных волн в вакууме:
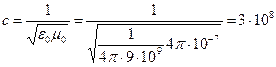 м/с.
м/с.
Таким образом, скорость распространения электромагнитных волн в вакууме совпадает со скоростью света. В среде скорость распространения электромагнитных волн уменьшается:
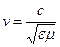 . .
| (24.12) |
Поскольку у большинства веществ (кроме ферромагнетиков) m» 1, то с большой степенью точности можно записать
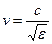 . .
| (24.13) |
Электромагнитные волны являются поперечными: векторы напряженности электрического (E) и магнитного (H) полей, а также направление скорости распространения электромагнитной волны образуют тройку взаимно перпендикулярных векторов (рис. 24.1). Заметим, что колебания электрического и магнитного полей в бегущей электромагнитной волне происходят в одинаковой фазе.
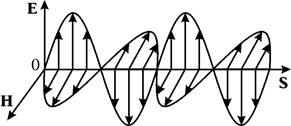
Рис. 24.1
24.2. Вектор Умова – Пойнтинга
При распространении электромагнитных вол происходит перенос энергии. Количественной характеристикой такого переноса служит вектор плотности потока энергии, который применительно к электромагнитным волнам называется вектором Умова-Пойнтинга.
В электромагнитной волне необходимо учитывать энергию электрического и магнитного полей, поэтому плотность энергии волны
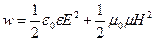 . .
| (24.14) |
Средние значения энергии электрического и магнитного полей равны:
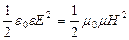 .
.
Отсюда
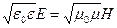 . .
| (24.15) |
С учетом (24.15) выражение для плотности энергии электромагнитной волны (24.14) можно преобразовать к виду
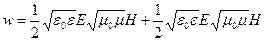 ;
;
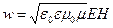 . .
| (24.16) |
Подставив (24.16) в выражение для плотности потока энергии (22.9), получим
или в векторной форме
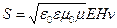 . .
| (24.17) |
С учетом (24.11) выражение (24.17) можно записать в виде 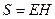
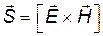 . .
| (24.18) |
Последнее выражение и представляет собой вектор Умова-Пойнтинга.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1565; Нарушение авторских прав?; Мы поможем в написании вашей работы!