Дифракция сферических волн (дифракция Френеля)

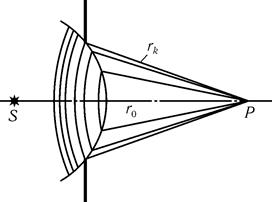Рис. 26.3

1. Дифракция на малом круглом отверстии. Пусть сферический фронт достигает непрозрачного экрана, в котором вырезано малое круглое отверстие (рис. 26.3). Необходимо найти интенсивность света в точке P, находящейся за экраном. Для простоты ограничимся случаем, когда прямая SP проходит через центр отверстия.

Предположим, что размеры отверстия таковы, что из точки P "видно" n зон Френеля. Тогда ряд (26.2) обрывается на n-м члене:

.

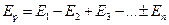(26.3)

Для вычисления суммы (26.3) Френель предположил, что в случае сферического фронта последовательность E₁, E₂,..., En — убывающая арифметическая прогрессия, т.е.

E1 > E2 >... > En

(26.4)

и, кроме того, на основании основного свойства арифметической прогрессии

Ei+1 – Ei = Ei – Ei-1.

(26.5)

Качественно соотношения (26.4) можно обосновать следующим образом. Несмотря на то, что площади зон одинаковы, их видимая площадь при наблюдении из точки P убывает по мере продвижения от центральной зоны к периферии по закону Sk = S1cos ak, где ak — угол между нормалью к k-й зоне и направлением на точку P. Если представить зоны как светящиеся полоски, то соответствующим образом будет убывать и вклад каждой из последующих зон в суммарную амплитуду колебаний в точке P.

Из (26.5) следует

.

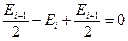(26.6)

С помощью (26.6) легко провести суммирование в (26.3). Результат зависит от того, четное или нечетное число зон открыто отверстием.

Пусть n — нечетное число. Для определенности возьмем n=5. Представим (26.3) в виде

.

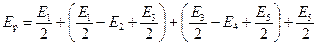Выражения в скобках в соответствии с (26.6) равны нулю, поэтому

.

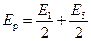В общем случае для нечетного n

.

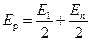Можно показать, что если открыто четное число зон Френеля, то

.

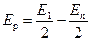Таким образом,

,

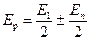(26.7)

причем знак "+" берется, если n — нечетное, и "–", если n — четное число.

Итак, в точке P наблюдается максимум интенсивности, если открыто нечетное число зон Френеля, и минимум, если открыто четное число зон. Поскольку с ростом n амплитуда En убывает, то по мере увеличения диаметра отверстия интенсивность максимумов будет уменьшаться. В пределе при n ® ¥ (экран отсутствует) En ® 0 и 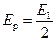, а интенсивность 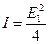. Если же размеры щели таковы, что открывается лишь первая зона Френеля, то в точке P наблюдается наиболее интенсивный максимум: .

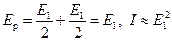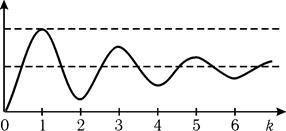Рис. 26.4 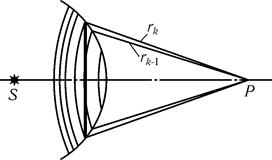Рис. 26.5

Качественно зависимость амплитуды колебаний в точке P от числа открытых зон Френеля показана на рис. 26.4.

2. Дифракция на непрозрачном круглом экране. Пусть непрозрачный круглый экран закрывает k-1 первых зон Френеля, так что из точки P виды все последующие зоны, начиная с k-й (рис. 26.5). Амплитуда колебаний в точке P

.

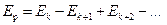Представив эту сумму в виде

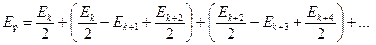Выражения в скобках в соответствии с (26.6) равны нулю, поэтому

.

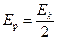(26.8)

Таким образом, в точке P (центре геометрической тени) будет наблюдаться светлое пятно. Интенсивность этого пятна убывает с увеличением размеров экрана (Ek ® 0 при k ® ¥), поэтому для достаточно больших экранов явление дифракции не наблюдается.

Дата добавления: 2015-06-04