Принцип Гюйгенса-Френеля. Расчет дифракционной картины методом зон Френеля

Дифракцией называется огибание волной малых препятствий (обычно соизмеримых с длиной волны) и проникновение ее в область геометрической тени. Дифракция света наблюдается при распространении световых волн вблизи резких краев непрозрачных или прозрачных веществ, при прохождении света через узкие отверстия и в среде с резкими неоднородностями.

Качественно явление дифракции можно объяснить с помощью принципа Гюйгенса: каждая точка волнового фронта — это источник вторичных сферических волн, огибающая которых представляет собой фронт волны в последующий момент времени.

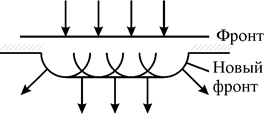Рис. 26.1

Рассмотрим применение этого принципа на примере дифракции света на узкой щели. Из рис. 26.1 видно, что вблизи краев щели новый фронт волны изгибается, вследствие чего свет заходит в область геометрической тени, т.е. наблюдается явление дифракции.

Однако принцип Гюйгенса не дает возможности ответить на вопрос, какова интенсивность света, зашедшего в область геометрической тени. Для ответа на этот вопрос нужно использовать более общий принцип Гюйгенса-Френеля. В его основу положен принцип Гюйгенса, который дополняется принципом когерентности вторичных сферических волн. С учетом этого принцип Гюйгенса-Френеля можно сформулировать следующим образом. Каждую точку волнового фронта в данный момент времени можно рассматривать как источник вторичных сферических волн, которые когерентны и поэтому могут интерферировать между собой. Фронт волны в последующий момент времени находится как огибающая вторичных сферических волн. Интенсивность света в данной точке определяется результатом интерференции вторичных волн, дошедших до этой точки.

Для вычисления интенсивности света в какой-нибудь точке пространства во многих случаях удобно пользоваться методом, разработанным Френелем (метод зон Френеля). Основная идея этого метода состоит в том, что фронт волны разбивается на зоны (участки) так, чтобы расстояние от краев соседних зон до рассматриваемой точки отличалось на l/2.

На рис. 26.2 показан пример построения зон Френеля для сферического фронта. Фронт волны рассекается на отдельные участки плоскостями, перпендикулярными к плоскости рисунка, так что

,

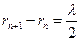(26.1)

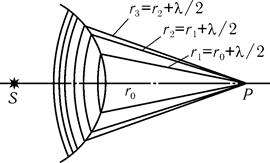Рис. 26.2

где rn — расстояние от края n-й зоны до рассматриваемой точки P.

Обозначим через Ei амплитуду электрического вектора световой волны, приходящей в точку P от i-й зоны. В точке P происходит сложение колебаний с амплитудами E₁, E₂, E₃,.... С учетом (26.1) можно утверждать, что соседние зоны "посылают" в точку P световые колебания в противофазе, поэтому результирующая амплитуда колебаний

.

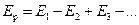(26.2)

Для нахождения знакопеременной суммы (26.2) следует ввести дополнительные предположения о соотношениях между амплитудами E₁, E₂, En,.... Эти соотношения зависят от вида волнового фронта световой волны и будут рассмотрены далее.

Дата добавления: 2015-06-04