Основные системы координат

R B

Dh

A T C

a

Рис. 2. Схема влияния кривизны Земли на измерения расстояний

Если допустить, что длина линии АВ равна 10 км, а радиус шара 6371км, то величина искажения (Dd) в длине линии из-за неучтенного влияния кривизны Земли будет равно примерно 1 см. Величина Dd называется абсолютной погрешностью определения длины (d) данной линии.

Абсолютные погрешности линейных измерений слабо характеризуют их с качественной стороны. Действительно, например, абсолютная погрешность измерения какой-либо линии равна 20 см. Хорошо или грубо измерена данная линия? Без сравнения со всей измеряемой длиной на это ответить затруднительно. К примеру, измерялась длина стола и была допущена абсолютная погрешность в измерении 20 см. Как же может быть оценено данное измерение, если длина стола составила 1,5 м? Очевидно, что данное измерение выполнено очень грубо. С другой стороны, с такой же абсолютной погрешностью было измерено расстояние до Луны (300 000 км). В этом случае, какую оценку можно дать нашему измерению? Очевидно, как отличную. Поэтому линейные измерения характеризуются, как правило, относительными погрешностями то есть отношением абсолютной погрешности ко всей измеряемой длине

. (3)

Относительная погрешность всегда выражается простой дробью, в числителе которой пишется единица, а в знаменателе число, полученное при делении всей длины на абсолютную погрешность.

В данном примере при измерении длины линии в 10 км под влиянием неучтённой кривизны Земли была допущена погрешность в 1 см.

Подставляя эти значения в формулу (3), получим относительную погрешность

.

По теории вероятности такая погрешность считается исчезающе малой величиной, а в геодезической практике её вообще не принимают во внимание.

Отсюда следует, что территория земной поверхности диаметром 20 км (10 км в одну сторону и 10 км в другую) может быть принята за плоскость.

Что касается влияния кривизны Земли на измерения вертикальных расстояний (Dh), то из анализа рис. 2 видно, приняв Dh за дугу радиуса d,

Dh = ad

или, с учётом a=d/R, будем иметь

. (4)

Если допустить, что расстояние между точками А и В составляет всего лишь 1 км, то ошибка в вертикальной длине составит 8 см, а при расстоянии 3 км составит уже 71 см.

В инженерной практике ошибка в определении высот допускается на 1 км хода не более 2-5 см. Отсюда следует, что даже при небольших горизонтальных расстояниях между точками не следует пренебрегать кривизной Земли.

Решив главную задачу геодезии, можно приступить к решению и остальных задач.

Для изучения земной поверхности с целью получения топографической информации о ней или решения инженерно-технических задач применяется метод проекций, который заключается в следующем. Изучаемые точки физической поверхности Земли проектируются на поверхность эллипсоида путём определения соответствующих величин в той или иной системе координат, связанной с математической формой и размерами Земли. В геодезии применяются различные системы координат. Остановимся на некоторых из них.

1.3.1. Система геодезических координат

В данной системе координат положение точек в пространстве определяется тремя величинами: геодезической широтой В, геодезической долготой L и геодезической высотой Н (рис.3). Геодезическая широта и долгота определяют положение точки на поверхности эллипсоида, а высота – расположение точки (А) земной поверхности относительно сфероида.

Рис. 3. Схема геодезических координат

Геодезической широтой B называется угол между нормалью к поверхности эллипсоида в данной точке и плоскостью геодезического экватора, то есть плоскостью, перпендикулярной к малой оси в центре эллипсоида.

Геодезической долготой L называется двугранный угол между плоскостью начального геодезического меридиана и плоскостью геодезического меридиана, проходящего через данную точку. Плоскость геодезического меридиана проходит через данную точку и малую ось, ось вращения эллипсоида.

Геодезической высотой Н называется расстояние между данной точкой и поверхностью эллипсоида по нормали к ней.

Геодезические координаты вычисляют по результатам геодезических измерений.

1.3.2. Система астрономических координат

Наряду с геодезическими координатами имеются астрономические координаты и , которые определяются из астрономических наблюдений.

Астрономической широтой называется угол между отвесной линией в данной точке и плоскостью небесного экватора.

Астрономической долготой называется двугранный угол между плоскостью начального меридиана и плоскостью астрономического меридиана, проходящего через данную точку. Плоскость астрономического меридиана проходит через отвесную линию в данной точке и ось вращения Земли

Широты В и отсчитываются от экватора к полюсам и изменяются от 0 до 90 градусов с указанием северной или южной широты (с.ш. или ю.ш.). Долготы L и отсчитываются от начального (Гринвичского) меридиана к востоку (в.д.) и западу (з.д.) и изменяются от 0 до 180 градусов.

Геодезические и астрономические координаты отличаются из-за несовпадения отвесных линий и нормалей к поверхности эллипсоида. Это отличие зависит от величины уклонения отвесных линий, которая в равнинных районах составляет около 5 секунд, в горных районах – 10-15 секунд, в аномальных случаях – до 40 секунд и более.

При мелкомасштабном картографировании этим различием можно пренебречь и значения широты и долготы считают координатами общей системы географических координат.

1.3.3. Пространственная прямоугольная

система координат

В настоящее время в геодезии сравнительно широко применяется система прямоугольных координат XYZ с началом в центре О земного эллипсоида (см.рис.3); ось Z совмещена с малой осью эллипсоида, оси Х и У располагаются в плоскости земного экватора – первая в сечении начального меридиана, вторая – перпендикулярна к ней слева от первой если смотреть по оси ZO. Положение точки А на поверхности эллипсоида в этой системе определяется координатами Х = О1, У = 1 2, Z = 2А_О и на поверхности Земли отметкой Н = А_ОА.

В этой системе целесообразно определять положение объектов на околоземных орбитах (ракет, искусственных спутников Земли) или планет Солнечной системы.

При выполнении геодезических работ на ограниченных территориях земной поверхности применение геодезической системы координат становится неудобным вследствие неодинаковых линейных размеров угловых единиц широт и долгот в разных точках и по различным направлениям.

Поэтому система плоских прямоугольных (декартовых) координат, позволяющих при математической обработке результатов геодезических измерений использовать формулы плоской геометрии и тригонометрии, является предпочтительней.

Х (С)

1У – СЗ 1 - СВ.

А

У_А

Х_А

(З) О У (В)

111 – ЮЗ 11 - ЮВ

(Ю)

Рис. 4. Схема плоских прямоугольных координат

Эту систему образуют две взаимно перпендикулярные прямые линии, лежащие в горизонтальной плоскости; одну из линий совмещают с меридианом, принимая её за ось абсцисс х с положительным направлением на север, а вторую – за ось ординат у с положительным направлением на восток (рис.4). За начало координат О принимается точка пересечения этих прямых. Такая система называется правой; четверти нумеруются по ходу часовой стрелки, начиная с первой северо-восточной четверти (рис.4).

При произвольном выборе начала координат подобная система называется частной. Её сравнительно широко применяют при решении отдельных инженерно-технических задач. Для перехода от частной системы координат к общей географической нужно знать координаты точки О и угол между положительным направлением оси Х и северным направлением меридиана.

1.3.4. Зональная прямоугольная система координат

Как отмечалось выше, наиболее рациональна в практическом отношении плоская прямоугольная система координат. Однако применить её на поверхности эллипсоида проблематично. Известно, что поверхность сфероида нельзя изобразить на плоскости без искажений, то есть невозможно соблюсти полного подобия геометрических построений на плоскости и поверхности эллипсоида. Поэтому найти такой закон изображения поверхности эллипсоида на плоскости проекции, искажения на которой были бы минимальны, является задачей первостепенной важности.

В настоящее время в картографии законов изображения поверхности эллипсоида на плоскости множество, что зависит от целевого назначения проекций. В геодезии желателен такой закон изображения, который обеспечивал всю территорию страны единой системой плоскихпрямоугольных координат, что приводит к единообразию математической обработки результатов измерений и единой системе создания топографических карт. При этом искажения на плоскости проекции должны быть минимальными или искажались бы не все элементы геодезических построений, а только некоторые из них, например, длины сторон, и чтобы в пределах определённой зоны масштаб изображения можно было считать постоянным. Такими свойствами обладают конформные проекции:

а) угловые искажения отсутствуют;

б) масштаб в данной точке одинаков по всем направлениям;

в) в пределах небольших участков масштаб можно считать практически постоянным;

г) изображение небольших участков подобно натуре.

Перечисленными свойствами обладает принятая в странах СНГ система плоских прямоугольных координат в проекции Гаусса-Крюгера. Гаусс предложил и обосновал эту проекцию, а Крюгер дал рабочие формулы для вычислений в этой проекции.

Система координат Гаусса-Крюгера определяется следующими условиями:

а) изображение на плоскости равноугольное;

б) осевой меридиан и экватор изображаются на плоскости проекции прямыми линиями, принимаемыми за оси абсцисс и ординат с началом координат в точке их пересечения;

в) масштаб вдоль осевого меридиана постоянен и принят равным единице.

В своей проекции, которая называется равноугольной поперечно-цилиндрической, Гаусс предложил поверхность эллипсоида делить меридианами на зоны шириной 6^о по долготе (рис.5).

Здесь возникает новое понятие меридиана – осевой, объяснение которому будет дано ниже.

Графически проекция Гаусса может быть объяснена следующим образом (рис.6).

.

	Р1

Рис. 5. Схема деления эллипсоида на зоны

В цилиндр соответствующего диаметра помещается сфероид таким образом, чтобы средний (осевой) меридиан зоны касался поверхности цилиндра, а крайние меридианы развертывались на поверхность цилиндра с минимальным искажением.

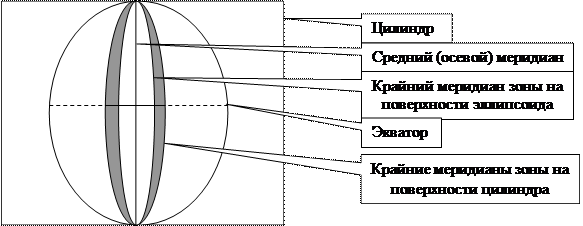Рис.6. Схема изображения зоны на поверхности цилиндра

Если прокатить сфероид (шар- для лучшего понимания геометрии проекции) по цилиндру, поворачивая его на 6^о и выделяя полученную зону на поверхности цилиндра, то после разрезания последнего вдоль полюсов и развёртки его на плоскость получим общую картину изображения эллипсоида в проекции Гаусса-Крюгера (рис.7).

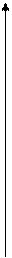Х Х Х Х Х Х

О

О

О

О

О

О

ОО

У

1 зона 2 зона 3 зона 4 зона 5 зона 6 зона

Рис.7. Схема изображения эллипсоида в проекции Гаусса – Крюгера

Как видим, в каждой зоне имеются две взаимно перпендикулярные прямые линии, отвечающие условию системы плоских прямоугольных координат. В каждой зоне осевой меридиан принимается за ось абсцисс, а экватор (общий для всех зон) за ось ординат с положительным направлением соответственно на север и восток. Линии, параллельные осевому меридиану и экватору, образуют координатную сетку. Таким образом, получена система плоских прямоугольных координат, жёстко привязанная к поверхности эллипсоида, - начало координат для каждой зоны имеет: широту В = 0, долготу L_O,N = N x 6^o – 3^o. Здесь N – номер зоны, Всего зон 60 и счёт их ведётся к востоку от Гринвича

Из анализа рис.6 видно, что наличие 60 зон приводит к тому, что разные точки (а, в, с, d) в разных зонах могут иметь одинаковые координаты. Чтобы избежать возникающей неопределённости и отрицательных значений ординат, немецкий учёный Баумгард предложил к величине ординаты прибавлять 500 км и к полученному результату приписывать номер зоны. Например, действительные координаты точки D в четвёртой зоне (см. рис.7) равны:

Х = 6 311 524 м, У = - 182 365 м.

По предложению Баумгарда эти координаты будут записаны:

Х = 6 311 524 м, У = 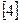317 635 м.

Как показали исследования, шестиградусные координатные зоны вполне удовлетворяют по точности мелкомасштабные съёмки. В проекции Гаусса-Крюгера искажения длин линий возрастают по мере удаления от осевого меридиана и достигают максимальных значений на краю зоны.

Величина искажения может быть рассчитана по формуле

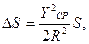(5)

где У_ср= , R – средний радиус кривизны, Х₁ У₁ и Х₂ У₂ – координаты концов отрезка S.

Искажения в длинах линий на краю зоны достигают в относительном выражении величин . Такие искажения недопустимы при крупномасштабных съёмках – при съёмке в масштабе 1:5000 и крупнее.

Решение этой проблемы было предложено Баумгардом, путём применения трёхградусных координатных зон с долготой осевых меридианов

L_О,n= n ●3⁰, (6)

где n – номер трёхградусной зоны.

В трёхградусной зоне максимальные искажения изображений в 4 раза меньше максимальных искажений шестиградусных зон.

В некоторых случаях для участков, расположенных на краях зон, целесообразно применять частные системы координат, принимая за осевой меридиан, линию в середине участка. Действительно, как показал анализ влияния кривизны Земли на измерения длин линий (см. рис.2), в пределах 20 км поверхность эллипсоида можно принимать за плоскость. В этом случае ошибка 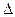d в длине d за не учет кривизны Земли может быть рассчитана по формуле

, (7)

где R – радиус Земли, принятого за шар.

При длине d = 10 км и R = 6371 км 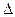d = 1 см, что в относительном выражении будет равно .

Эта величина соответствует максимальной точности при измерении расстояний на земной поверхности. Отсюда следует, что в практическом отношении, особенно, на краях зоны целесообразно использовать частные плоские прямоугольные системы координат.

Дата добавления: 2015-06-04