Масштабы. Точность масштабов

План и карта. Профиль

ТОПОГРАФИЧЕСКИЕ КАРТЫ И ПЛАНЫ

Картой называется уменьшенное изображение на плоскости значительной части земной поверхности, построенное по определенным математическим законам (проекция Гаусса), учитывающим кривизну Земли. На топографических картах в отличие от географических изображаются значительно меньшие участки местности, но с большей точностью и подробностью, что позволяет решать на них различные инженерно-геодезические задачи, возникающие при проектировании сооружений. Ещё большая подробность и точность изображения земной поверхности достигается на топографических планах.

Планом называется уменьшенное и подобное изображение горизонтальной проекции участка земной поверхности. При этом кривизна Земли не учитывается (проекция Гаусса-Крюгера).

Профиль – это уменьшенное изображение вертикального разреза местности, выполненное в двух масштабах: по горизонтальной оси или оси расстояний принимается значение одного масштаба, а по вертикальной оси или оси высот выбирается масштаб значительно крупнее для более рельефного изображения перегибов местности (обычно вертикальный масштаб в 10 раз крупнее горизонтального).

Степень уменьшения линий на плане или карте относительно горизонтальных проложений соответствующих линий на местности называется масштабом. Масштаб карты можно определить из отношения

, (15)

где L – длина горизонтальной проекции линии на местности; l - длина этой же линии на карте.

В геодезии масштаб выражают простой дробью, в числителе которой всегда единица, а в знаменателе число М, показывающее, во сколько раз длина отрезка на карте меньше длины этого же отрезка на местности. Такой масштаб называется численным.

На картах и планах численный масштаб подписывается ниже чертежа, а под ним даётся его расшифровка. Например, масштаб карты 1: 25000. а ниже можно прочитать «в 1 см плана 250 метров на местности».

В России установлены следующие основные масштабы топографических карт и планов:

1: 1000 000 - в 1 см 10 км Топографические

1: 100 000 - в 1 см 1 км

1: 50 000 - в 1 см 500 м карты

1: 25 000 - в 1 см 250 м

1: 10 000 - в 1 см 100 м

1: 5 000 - в 1 см 50 м Топографические

1: 2 000 - в 1 см 20 м

1: 1 000 - в 1 см 10 м планы

1: 500 - в 1 см 5 м

Зная численный масштаб карты, можно определить длину линии на местности, измерив её величину на карте. Например, на карте масштаба 1:25000 измерен отрезок l = 3,54 см. Тогда длина соответствующего ему горизонтального отрезка на местности может быть определена из пропорции:

l см - 250 м,

3,54 см - L м, (16)

отсюда L= 3,54 x 250 = 885 м.

Аналогично решается и обратная задача, когда измерен горизонтальный отрезок на местности L и его необходимо нанести на карту, то пропорция решается в отношении величины l.

При массовых измерениях и построениях пользоваться формулой (16) не всегда целесообразно, а порой и невозможно (при работе с планом крупного масштаба). Действительно, если взять отрезок длиной, например, 3,54 см, то построить его на плане крупного масштаба проблематично. Кроме того, при массовых измерениях объём таких построений будет значительным. Поэтому при работе с картой используется так называемый линейный масштаб, который практически решает пропорцию (16) графическим способом. Для этого на прямой несколько раз откладывается отрезок длиной 1 или 2 см, называемым основанием масштаба (рис.14).

а в

500 0 500 1000 1500 2000 2500

1:25000 основание

в 1 см 250 метров масштаба

2 см

Рис.14. Схема линейного масштаба

Крайний левый отрезок делят на 10 равных частей. Соответственно заданному численному масштабу подписывают каждое деление линейного масштаба. Например, для численного масштаба 1:25000 при основании линейного масштаба 2 см. (см. рис.14) каждое деление справа будет равно 500 м, а каждое деление левого отрезка равно соответственно 50 м, на глаз можно определять десятые доли деления, то есть 5 м.

Пользуются линейным масштабом следующим образом. Зафиксировав измерителем отрезок на карте, правую ножку его устанавливают на штрих одного из основных делений так, чтобы другая ножка попала на основание левее 0 (нулевого деления). На рис.14 расстояние между концами ножек циркуля равно 2650 м. В случае несовпадения конца левой ножки с целым делением доли его определяют на глаз.

Линейный масштаб по сравнению с обычной линейкой с миллиметровыми делениями не повышает точности определения длин отрезков, но позволяет отказаться, как отмечалось выше, от решения пропорций и при многочисленных измерениях повысить производительность работ по определению длин отрезков. Точность определения длин линий по линейному масштабу составляет примерно 0,2 деления. Если в основании линейного масштаба принят отрезок в 1 см, то графическая точность (t_л)линейного масштаба будет равна 0,2 мм. Такая точность измерений вполне устраивает исполнителей при работе с картой и не допустима при работе с планом. Чтобы убедиться в этом, следует рассмотреть понятие точности масштабов и производимых измерений.

Точность численного масштаба (t_ч) определяется графической точностью (t_гр) построения любого плана или карты, величина которого принимается равным 0,1 мм, точнее этого отрезки на плане не могут быть изображены. Отсюда следует, что точностью численного масштаба называется горизонтальный отрезок на местности, соответствующий 0,1 мм на карте или плане,

t_ч = t_гр х М. (17)

Следовательно, точности указанных выше численных масштабов будут равны:

1: 1 000 000 t = 0,1 мм х 1 000 000 = 100 000 мм = 100 м

1: 100 000 t = 0,1 мм х 1 00 000 = 10 000 мм = 10 м

1: 50 000 t = 0,1 мм х 50 000 = 5 000 мм = 5 м

1: 25 000 t = 0,1 мм х 25 000 = 2500 мм = 2,5 м

1: 10 000 t = 0,1 мм х 10 000 = 1000 мм = 1 м

1: 5000 t = 0,1 мм х 5000 = 500 мм = 0,5 м = 50 см

1: 2000 t = 0,1 мм х 2000 = 200 мм = 0,2 м = 20 см

1: 1000 t = 0,1 мм х 1000 = 100 мм = 0,1 м = 10 см

1: 500 t = 0,1 мм х 500 = 50 мм = 0,05 м = 5 см

Отсюда можно рассчитать точность измерений (построений) длин линий на той или иной карте или плане с использованием линейного масштаба. Как отмечалось выше, графическая точность линейного масштаба равна примерно 0,2 наименьшего деления его. Следовательно, для линейного масштаба с основанием его 1 см графическая точность определения длины отрезка будет равна 0,2 мм, что в 2 раза грубее точности численных масштабов. Если учесть, что в соответствии с теорией вероятности предельная ошибка измерения длин линий может быть в 2-3 раза больше случайной, то точность измерений (построения) длин линий резко падает. Отсюда видно, что глазомерная оценка части делений линейного масштаба снижает точность измерительных работ на планах и картах, особенно при использовании линейных масштабов, в основании которых положен отрезок 2 см и более. Чтобы избежать оценки делений на глаз и повысить точность определения длин линий на карте (плане), применяют поперечный масштаб, называемый в обиходе масштабной линейкой. Он строится на основе линейного масштаба.

Для этого на прямой откладывают несколько раз отрезок, равный 1 или 2 см, как это было сделано при построении линейного масштаба. Из полученных точек восстанавливают перпендикуляры к этой прямой (рис.15). Крайнее левое основание делят на десять равных частей, а на перпендикулярах откладывают десять таких же делений. Через полученные на перпендикулярах точки проводят параллельные линии. Левое крайнее деление на верхней линии также разбивается на десять равных частей, которые соединяются прямыми с нижними следующим образом: нулевое деление на нижнем основании соединяется с первым на верхнем, первое на нижнем основании со вторым на верхнем. Отрезок “ав” называется наименьшим делением поперечного масштаба или его точностью (t_п), он будет равен 1:100 длины основания масштаба. Такой поперечный масштаб называется нормальным или сотенным. Точность поперечного масштаба может быть вычислена по формуле

t_п = 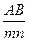, (18)

где АВ – величина основания, в см, m - число делений в крайнем левом основании, n - число горизонтальных линий, считая первую линию за 0.

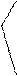а в

100 70 50 30 10 0 100 200

1:10 000

в 1 см – 100 метров

Рис.15. Схема поперечного масштаба

Если основание масштаба равно 1 см и оно поделено на m=10, а число горизонтальных линий n=10, то точность такого поперечного масштаба будет равно t_п = 1 см/10 х 10 = 0,1 мм, его точность соответствует точности численного масштаба. Если в основании поперечного масштаба будет 2 см и более, то точность определения длины отрезков плана или карты соответственно снизится. Кроме того, все рассуждения о точности поперечного масштаба относятся к масштабным линейкам, изготовленным в заводских условиях с гравировкой линий на металле. Если поперечный масштаб построен графическим путём, то им пользоваться нельзя, так как точность его будет сведена практически к точности линейного масштаба.

Если принять на схеме длину основания 1 см, то поперечный масштаб будет подписан так, как это показано на рис.15. Наименьший отрезок “ав” (на второй горизонтальной линии) будет равен 1 м. Процесс определения длины отрезка, измеренного на карте масштаба 1:10 000, заключается в следующем.

Зафиксировав измерителем отрезок на карте или плане, правую ножку его устанавливают на штрих одного из основных делений так, чтобы другая ножка попала на основание левее нулевого деления (как поступали в случае с линейным масштабом). Если левая ножка циркуля не совпала с целым делением (см. рис.15, вертикальная линия), то циркуль перемещается поступательно вверх до совмещения левой ножки с наклонной линией основания. Длина линии равна сумме отрезков от нулевого деления до правой ножки циркуля плюс число полных малых делений левого основания и плюс число наименьших делений «ав», соответствующее номеру горизонтальной линии, на которой расположены иглы измерителя. На рис.15 расстояние между ножками циркуля в указанном масштабе равно 200 м плюс 60 м и плюс 4 м, то есть 264 м.

Как отмечалось выше, основание поперечного масштаба равно 1 или 2 см. Однако иногда целесообразно брать иной размер основания. Так 1 см рационально брать для численных масштабов 1:1000 и 1:10 000, 2 см для масштабов 1: 500, 1:5000 и 1:50 000, 4 см – 1:25 000, 5 см – 1:2000. Тогда основание масштаба будет кратно 10 м, 100 м и 1000 м.

Дата добавления: 2015-06-04