
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция № 6
|
|
|
|
Тема: О теории предельного напряженного состояния грунтов и ее приложениях.
Ключевые слова: Теория предельного равности, структурная прочность грунта, фаза напряженного состояния грунта, фаза уплотнения, силы внутреннего сопротивления, фаза сдвигов, диаграммы предельных напряжений, условие предельного равновесия, начальной критической нагрузки, вертикальное напряжение от собственного веса грунта, начальное критическое давление, расчетное сопротивление грунта, подошвы фундамента, расчетное значение удельного сцепления грунта, глубина заложения фундаментов, предельные нагрузки, критическая нагрузка, линий скольжения, осесмметричные задачи, устойчивость откосов и склонов, насыпи, выемки, дамбы, земляные плотины, эрозионные процессы, нарушение равновесия, коэффициент устойчивости откоса, крутизна откоса, подпорные стенки, активная давления грунта.
Напряженное состояние в какой-либо точке грунта рассматривается как предельное в том случае, когда незначительное добавочное силовое воздействие нарушает равновесие и приводит грунт в неустойчивое состояние. Такое напряженное состояние рассматривается как совершенно недопустимое при строительстве зданий и сооружений. Поэтому необходимо в каждом конкретном случае определять максимально возможную нагрузку на грунт, при которой он будет находиться в состоянии устойчивого равновесия.
Прочность (несущая способность), устойчивость и давление грунтов на ограждения являются частными задачами теории предельного равновесия, ее приложением.
Вся теория предельного равновесия применима только к плотным грунтам. В рыхлых, лессовых просадочных и других грунтах с неустойчивой структурой задолго до предельного равновесия развиваются недопустимо большие деформация. Расчеты ведут уже по ним.
Фазы напряженного состояния грунтов при возрастании нагрузки. При воздействии на грунт местной постепенно возрастающей нагрузки он испытывает сложное напряженное состояние, которое в значительной степени отличается от

|
 компрессионного сжатия. g лом случае
компрессионного сжатия. g лом случае
грунт кроме нормальных испытывает и касательные
напряжения, которые при достижении определенной
величины могут вызвать необратимые скольжения
(сдвиги).
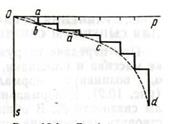
На рис. 6.1 приведена кривая деформаций грунта
при действии постепенно возрастающей местной нагрузки.
Рис. 6.1. График зависимости осадки от нагрузки
Пока внешней нагрузкой не превзойдена структурная прочность грунта, он испытывает незначительные деформации, которые вполне упруги и поэтому полностью восстанавливаются после снятия давления. С увеличением нагрузки (за пределом структурной прочности) возникает уплотнение грунта, сопровождающееся уменьшением пористости под нагруженной поверхностью. Эта фаза напряженного состояния грунта называется фазой уплотнения. В строительном отношении фаза уплотнения не представляет собой никакой опасности, так как грунт приобретает более плотную структуру и осадки его невелики. В пределах фазы уплотнения зависимость осадки от нагрузки для практических целей можно принять прямолинейной.
Дальнейшее увеличение нагрузки приводит к тому, что в отдельных точках грунта силы внутреннего сопротивления оказываются недостаточными, и между частицами грунта возникают скольжения, которые формируются в площадки скольжения и зоны сдвигов. Так наступает вторая фаза — фаза сдвигов. В этой фазе рост осадок значительно опережает увеличение внешней нагрузки, поэтому зависимость между деформациями н напряжениями имеет нелинейный характер. Последующее увеличение нагрузки сопровождается пластическими или прогрессирующими деформациями, которые совершенно недопустимы для зданий и сооружений.
Конец фазы уплотнения и начало фазы сдвигов соответствуют начальной критической нагрузке на грунт. В конце уплотнения под штампом начинает формироваться жесткое ядро ограниченных смещений частиц. Это ядро работает как клин, разжимает грунт в стороны и обусловливает значительные осадки штампа. Исходя из опытов проф. В. Г. Березанцева и В. А. Яро-шенко, уплотненное ядро полностью сформировывается при достижении грунтом максимальной несущей способности. В дальнейшем ядро остается неизменным. При этом напряженном состоянии преобладают боковые смещения частиц, формируются непрерывные поверхности скольжения и толща грунта теряет устойчивость.
 Уравнения предельного равновесия для сыпучих и связных. При передаче нагрузки на поверхность грунта в любой точке массива и площадки, проведённой через эту точку под углом а, возникнут нормальные и касательные напряжения (рис. 6.2). К нормальным напряжениям следует отнести и силы связности ре. В общем случае на площадку mm будут действовать напряжения нормальные
Уравнения предельного равновесия для сыпучих и связных. При передаче нагрузки на поверхность грунта в любой точке массива и площадки, проведённой через эту точку под углом а, возникнут нормальные и касательные напряжения (рис. 6.2). К нормальным напряжениям следует отнести и силы связности ре. В общем случае на площадку mm будут действовать напряжения нормальные  и касательные
и касательные 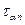 . Угол 0 называется углом отклонения.
. Угол 0 называется углом отклонения.
Условие предельного равновесия в данной точке выразится так:
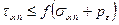 (6.1)
(6.1)
или
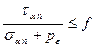 ,
,
где  — постоянная величина, которая в предельном состоянии представляет собой тангенс угла наклона прямолинейной огибающей кругов предельных напряжений. С другой стороны,
— постоянная величина, которая в предельном состоянии представляет собой тангенс угла наклона прямолинейной огибающей кругов предельных напряжений. С другой стороны,
 .
.  (6.2)
(6.2)
Так как через заданную точку можно провести множество площадок (аналогичных площадке mm), то надо выбрать самую невыгодную, для которой будет существовать 0max. Тогда
 .
.
 |
Рис. 6.2. Диаграммы предельных напряжений:
а — схема напряжений в данной точке;
б — диаграмма предельных напряжений для сыпучих грунтов;
в — та же, для связных
Рассмотрим условия предельного равновесия для сыпучих и связных грунтов. Для сыпучих грунтов угол отклонения принимает максимальное значение в том случае, когда огибающая коснется круга предельных напряжений.
Из  ОЕС sin
ОЕС sin  =EC/OC; EC=
=EC/OC; EC= 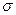 l—
l—  3/2;
3/2;
 .
.
Тогда
 . (6.4)
. (6.4)
Это и есть условие предельного равновесия для сыпучих грунтов. После несложных тригонометрических преобразований этому выражению можно придать другой вид:

или
 . (6.5)
. (6.5)
Это выражение широко используется в теории давления грунтов на ограждения.
Для связных грунтов
 ; (6.6)
; (6.6)
 .
.
Представим это уравнение в следующем виде:
 . (6.7)
. (6.7)
Так как pe=c/tg  , то можно записать:
, то можно записать:
 . (6.8)
. (6.8)
Эта формула широко применяется в задачах теории предельного равновесия.
Рассмотрим дифференциальные уравнения равновесия грунтов в предельно-напряженном состоянии для случая плоской задачи. Как известно из теории упругости, для этого случая дифференциальные уравнения равновесия линейно-деформируемых тел при горизонтальной ограничивающей полупространство плоскости записываются в следующем виде (направление оси У — горизонтально, z — вертикально):
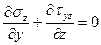 ; (6.9)
; (6.9)
 ,
,
где  — составляющие напряжений; у — удельный вес грунта.
— составляющие напряжений; у — удельный вес грунта.
В данных дифференциальных уравнениях три неизвестных, и поэтому задача (без добавочных условий) статически неопределима. Следует добавить третье уравнение — условие предельного равновесия для составляющих  :
:
 . (6.10)
. (6.10)
С учетом этого условия задача становится статически определимой. Решение этой задачи получено проф. В. В. Соколовским как системы уравнений гиперболического типа.
По аналогии рассматриваются и дифференциальные уравнения для случая пространственной задачи.
Определение начальной критической нагрузки. Как отмечалось ранее, при передаче постепенно возрастающей местной нагрузки выделяются две критические нагрузки на грунт: первая — начальная критическая и вторая — предельная.
Для определения первой рассмотрим действие равномерно распределенной нагрузки р на полосе шириной b при наличии боковой пригрузки q=yh (где у — удельный вес грунта и h — глубина заложения нагруженной поверхности) (рис. 6 .3).
Вертикальное напряжение от собственного веса грунта в точке М
 . (6.11)
. (6.11)
Необходимо найти такое значение начальной критической нагрузки нач ркр, при котором области предельного равновесия (зоны сдвига) только зарождаются. Эти зоны появляются, в первую очередь, у краев полосообразной нагрузки, так как
в этом месте наблюдается концентрация касательных напряжений.
Примем допущение о гидростатическом распределении напряжений от собственного веса грунта
 . (6.12)
. (6.12)
Запишем выражение главных напряжений в точке М с учетомдействия собственного веса грунта как сплошной нагрузки:
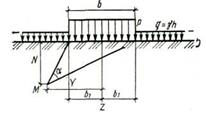 Рис. 6.3. Схема для определения
первой критической нагрузки на
грунт Рис. 6.3. Схема для определения
первой критической нагрузки на
грунт
|  ; (6.13) ; (6.13)

|
Подставив эти значения в условие предельного равновесия для связных грунтов, получим
 . (6.13а)
. (6.13а)
Это выражение можно рассматривать как уравнение граничной области предельного равновесия, а z — как ординату этой области. Решив это уравнение относительно z, найдем его максимальное значение (взяв первую производную dz/da и приравняв ее к нулю) и найдем cos a=sin 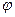 или
или  =
=  /2—
/2— 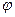 , sin (
, sin ( /2—
/2— 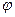 ) =cos ф.
) =cos ф.
Решая его относительно р=рКр, получим
 . (6.14)
. (6.14)
При отсутствии зон предельного равновесия следует полагать Zmax=0. Из этого условия определяется начальное критическое давление
нач  . (6.15)
. (6.15)
Эта формула известна в механике грунтов как формула проф. Н. П. Пузыревского. Определяемое по ней давление можно рассматривать как совершенно безопасное и никаких добавочных коэффициентов вводить не следует.
Для идеально связных грунтов (у которых  ,
,  ) выражение для нач ркр получается следующим образом. Условие предельного равновесия для таких грунтов
) выражение для нач ркр получается следующим образом. Условие предельного равновесия для таких грунтов
 , (6.16)
, (6.16)
откуда
 .
.
Подставив выражения для главных напряжений при  =0, получим
=0, получим
 . (6.17)
. (6.17)
Это выражение будет иметь максимум при sin  =l, когда состояние предельного равновесия начнет зарождаться под краем фундамента:
=l, когда состояние предельного равновесия начнет зарождаться под краем фундамента:
Нач  . (6.18)
. (6.18)
Полученная формула используется часто для определения безопасного давления для глинистых грунтов с малым углом внутреннего трения ( ...7°).
...7°).
Согласно СНиП 2.02.01—83 расчетное сопротивление грунта основания
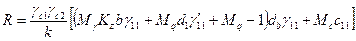 , (6.19)
, (6.19)
где Yс1 и Yc2— коэффициенты условий работы, принимаемые по таблицам СНиПа; k — коэффициент (при определении прочностных характеристик непосредственными испытаниями k=l; если они принимаются по таблицам, то  =1,1); Mv; Mq, Mc — коэффициенты, принимаемые по таблице; Кz — коэффициент (при b<10 м Kz=1, при b
=1,1); Mv; Mq, Mc — коэффициенты, принимаемые по таблице; Кz — коэффициент (при b<10 м Kz=1, при b 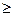 10 м Kz=Zo/b+O,2, здесь z0=8 м); Ь — ширина подошвы фундамента, м; уи — осредненное расчетное значение удельного веса грунтов, залегающих ниже подошвы фундамента, кН/м3; у11' — то же, залегающих выше подошвы фундамента; с11 — расчетное значение удельного сцепления грунта, залегающего непосредственно под подошвой фундамента, кПа; d1 — глубина заложения фундаментов бесподвальных сооружений или приведенная глубина заложения наружных и внутренних фундаментов от пола подвала,
10 м Kz=Zo/b+O,2, здесь z0=8 м); Ь — ширина подошвы фундамента, м; уи — осредненное расчетное значение удельного веса грунтов, залегающих ниже подошвы фундамента, кН/м3; у11' — то же, залегающих выше подошвы фундамента; с11 — расчетное значение удельного сцепления грунта, залегающего непосредственно под подошвой фундамента, кПа; d1 — глубина заложения фундаментов бесподвальных сооружений или приведенная глубина заложения наружных и внутренних фундаментов от пола подвала,
 , (6.20)
, (6.20)
где hs — толщина слоя грунта выше подошвы фундамента со стороны подвала, м; hCf — толщина конструкции пола подвала, м; h Cf — расчетное значение удельного веса конструкции пола подвала, кН/м3; db-глубина подвала — расстояние от уровня планировки до пола подвала, м (для сооружений с подвалом шириной b 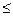 20 м и глубиной более 2 м принимается dь=2 м; при ширине подвала b>20 м принимается db=0).
20 м и глубиной более 2 м принимается dь=2 м; при ширине подвала b>20 м принимается db=0).
Предельные нагрузки для сыпучих и связных грунтов. Вторая критическая нагрузка рассматривается как предельная нагрузка, соответствующая полному исчерпанию несущей cпособности грунта и сплошному развитию зон предельного равновесия.
Величину предельной нагрузки можно оценить достаточно строго при наличии точных очертаний поверхностей скольжения. В свою очередь найти математически точные очертания поверхностей скольжения представляется возможным путем решения дифференциальных уравнений равновесия совместно с условиями предельного равновесия.
Для математического решения этой задачи используют приближенный прием. Он заключается в том, что задаются такими очертаниями поверхности скольжения, которые практически совпадают с точными, полученными из результатов численного решения системы дифференциальных уравнений предельного равновесия.
Этот прием широко использован проф. В. Г. Березанцевым (1952—1960) по определению предельной нагрузки в условиях плоской и осесимметричной задачи с учетом жесткого ядра. На основании опытных данных очертание жесткого ядра принимается В. Г. Березанцевым в виде прямоугольного треугольника (плоская задача) или конуса (осесимметричная пространственная задача) с углом при вершине 90°. Заглубление фундаментов учитывается действием боковой пригрузки q=yh, поэтому это решение применимо только для малозаглубленных фундаментов при h/b 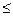 0,5.
0,5.
Для плоской задачи принята схема линий скольжения, представленная на рис. 6.4.
В треугольниках obc и О1b1c1 — два семейства сопряженных прямых, наклоненных к горизонтали под углом + ( /4—
/4— 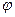 /2), в секторе oab и O1b1c1 — пучки прямых, исходящих из точек о и О1 и пересекающих их логарифмических спиралей. Угол наклона жесткого ядра к вертикали принят равным
/2), в секторе oab и O1b1c1 — пучки прямых, исходящих из точек о и О1 и пересекающих их логарифмических спиралей. Угол наклона жесткого ядра к вертикали принят равным  .
.
Для рассматриваемой схемы линий скольжения предельное сопротивление грунта
Пред.  , (6.21)
, (6.21)
где Nyn, Nqn, Ncn — коэффициенты несущей способности для плоской задачи, приведенные в таблицах; Ь1 — полуширина полосообразной

Рис. 6.4. Схема линий скольжения с учетом уплотненного ядра (плоская задача)

Рис. 6.5. Очертание линий скольжения с учетом уплотненного ядра (пространственная задача)
нагрузки; q=yn — боковая пригрузка; с — удельное сцепление грунта.
Приближенное очертание обертывающих поверхностей скольжения в случае пространственной осесимметричной задачи для фундаментов мелкого заложения с учетом уплотненного ядра приведено на рис.6.5.
Максимальное предельное сопротивление грунта
пpeд Nk=Nykybl+Nqkq+NckC, (6.22)
где Nyh, Nqk, Nсk — коэффициенты несущей способности для осесимметричной задачи (приводятся в таблице); Ь1 — половина стороны квадратной или радиус круглой подошвы фундамента. Для фундаментов средней глубины заложения (0,5<h/b<2) и глубокого заложения (h/b>2) заменять влияние глубины заложения действием боковой пригрузки не представляется возможным ввиду специфики механических явлений, происходящих в этом случае.
Сопоставляя результаты определения несущей способности основания по опубликованным экспериментальным данным и на основе приведенных формул, можно констатировать:
1) для идеально связных глинистых грунтов наблюдается практически полное совпадение экспериментальных и теоретических данных;
2) значения максимальной несущей способности оснований по результатам опытных данных в 1,5...2,5 раза превышают расчетные, что свидетельствует о необходимости дальнейших исследований для уточнения строгих методов расчета.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1851; Нарушение авторских прав?; Мы поможем в написании вашей работы!