Напряжений

Распределение давлений по подошве фундаментов (контактная задача). Для определения расчетных изгибающих моментов и поперечных сил в фундаментных балках, гибких фундаментах необхо­димо рассчитать реактивное, или, как его обычно называют, контактное, давление.

Исходным уравнением для решения этой задачи является формула Буссинеска для вертикальной деформации s_z от дейст­вия сосредоточенной силы [формула (4.8), рис. 4.10].

Для произвольной площадки будем иметь

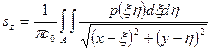, (4.20)

где А — площадь загрузки, по которой производится интегри­рование.

У абсолютно жесткого фундамента все точки подошвы име­ют равную вертикальную деформацию. Решение этого интег­рального уравнения при центральной нагрузке круглого абсо­лютно жесткого фундамента имеет вид

, (4.21)

где 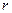— радиус подошвы фундамента; р — расстояние от центра подошвы до любой его точки; р_т— среднее давление на едини­цу площади фундамента.

Для случая плоской задачи

, (4.22)

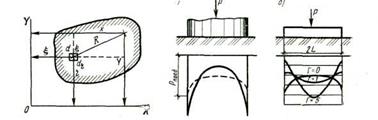Рис. 4.10. Схема за- Рис. 4.11. Эпюры контактных
грузки произвольно вы- давлений:

бранной площадки а — по подошве абсолютно жесткого фундамента;

б — по подошве фундаментов различной гибкости

где у — расстояние по горизонтали от середины фундамента до рассматриваемой точки; Ь₁ — полуширина фундамента.

С учетом формул можно построить эпюру контактных дав­лений по подошве для абсолютно жесткого фундамента (рис.4.11).

При р=г и y=bi р_ху= .

По центральной оси симметрии у фундамента круглой по­дошвы

р_о=р_т/2, (4.23)

у ленточного фундамента

р_й=2р_т/ 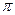. (4.24)

Решения, полученные с учетом плотности сухого грунта (Н. X. Арутюнян) и возрастанием по глубине модуля общей де­формации грунта (Ю. К. Зарецкий), свидетельствуют о том, что контактные давления по подошве жесткого фундамента рас­пределяются по более пологой кривой. Кроме того, у края фун­дамента контактные давления не могут быть больше предела несущей способности грунта, что также перераспределяет дав­ление по подошве (пунктирная линия на рисунке). Указанная концентрация напряжений у жестких фундаментов сказывается лишь на небольшую глубину от подошвы, вследствие чего об­щий характер напряжений мало изменяется, и поэтому осадка жесткого фундамента незначительно отличается от гибкого.

Для фундаментов конечной жесткости эпюры контактных давлений могут принимать очертание от седлообразного до па­раболического.

Распределение контактных давлений в значительной степе­ни зависит от гибкости фундамента Г, которая по М. И. Горбунову-Посадову равна

, (4.25)

где Е, v — модуль общей деформации и коэффициент попереч­ного расширения грунта основания; Е₁, 1₁ — жесткость фунда­ментной балки; h₁ — высота прямоугольной фундаментной балки.

На рис. 2.6,б даны три кривые распределения контактных давлений при гибкостях балки Г=0; 1; 5.

Распределение контактных давлений зависит не только от гибкости фундаментов, но и от глубины их заложения, внешней нагрузки и от прочностных характеристик грунтов основания.

Распределение напряжений от собственного веса грунта. Напряженияот собственного веса грунта (или природные давления) определяются для оценки природной уплотненности грунтов и свеженасыпанных земляных сооружений.

Напряжения от собственного веса по горизонтальной поверх­ности грунта увеличиваются с глубиной и равны

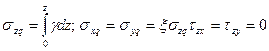, (4.26)

где =v/(1 —v)—коэффициент бокового давления в состоянии покоя; у — удельный вес грунта.

При постоянном удельном весе грунта

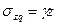. (4.27)

Длягрунтовой массы, т. е. водонасыщенного грунта с нали­чием свободной воды,

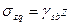, (4.28)

где y_sb — удельный вес грунта с учетом взвешивающего дейст­вия воды.

Эпюры распределения вертикальных давлений от собствен­ного веса грунта даны на рис. 4.12.

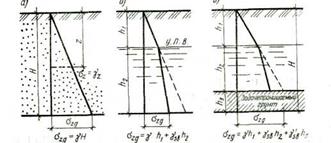Рис. 4.12. Эпюры вертикальных напряжений от соб­ственного веса грунта:

о — однородный грунт; б — при стоянии подземных вод на

глубине hi от поверхности земли; в — при расположении на

глубине hi+h₂ водонепроницаемого грунта

Дата добавления: 2015-06-04