Кубит. Определения. Свойства. Результат измерения кубита. Однокубитовые гейты

Уравнение Паули.

Классический бит может находиться в состоянии либо «0», либо «1», третьего, как говориться, не дано. Стало быть, единственное, что с битом можно сделать, это изменить его состояние на противоположное. Маленькое уточнение: на самом деле можно ещё принудительно установить бит в состояние «0» или «1». Это операции записи, мы их будем применять, конечно, но в число гейтов включать не будем. Также оставим за скобками вариант, формально эквивалентный применению «единичного» гейта, а на практике заключающийся в том, чтобы не делать с битом или кубитом ничего. Итак, с учётом уточнения, существует только один однобитный гейт – «NOT». Кубит может находится в квантовой суперпозиции групп витруальных вариантов |0〉 и |1〉:
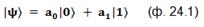«Доля» каждой из групп определяется двумя комплексными числами - амплитудами вероятности a₀ и a₁. Эти числа могут быть, в принципе, любыми. Значит, для кубита количество возможных квантовых состояний вида |ψ〉бесконечно.

Также бесконечно количество разрешенных однокубитных операций, которые, по сути дела, просто определённым образом изменяют значения амплитуд вероятности a₀ и a₁. При моделировании квантового компьютера будем считать, что мы умеем совершать над кубитом всевозможные однокубитные операции. Единственное ограничение, накладываемое квантовой физикой на такие операции, это требование унитарности. Глубого копать в сторону понятия унитарности нам резона нет, но заметим, что унитарность обеспечивается обратимыми операциями, которые мы изучали в предыдущей части. Для более продвинутых скажем, что унитарные операции математически идентичны повороту вектора квантового состояния в условном пространстве, без изменения длины (модуля) вектора. На практике операции реализуются путём «дозированных» физических воздействий на кубит. Любое такое воздействие, напомню, описывается матрицей следующего вида: Два числа в верхней строке показывают, как воздействие-операция изменяет группу |0〉. Два числа в нижней строке показывают, как изменяется группа |1〉. То есть, в общем случае для описания любой однокубитной операции достаточно этого набора из четырёх чисел. Для удобства некоторым, наиболее часто используемым операциям и их матрицам, присвоены особые обозначения.
Например, гейт [X], он же - квантовый «NOT» – гейт, описывается вот такой матрицей:

Давайте ещё раз постмотрим, как гейт [X] воздействует на состояние |ψ〉 (ф. 24.1.):

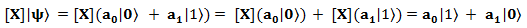
В результате воздействия [X] группы |0〉 и |1〉 «обменялись» амплитудами вероятности. Или можно взглянуть на это дело в другом ракурсе: воздействие [X] превратило группу |0〉 в группу |1〉, а группу |1〉, наоборот, в группу |0〉. Для полной ясности изобразим действие гейта [X] на следующей диаграмме:

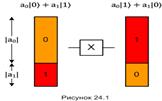
В дальнейшем нам предстоит рисовать квантовые вычислительные схемы. Они по виду будут аналогичны классическим схемам. В частности, однокубитные операции будем изображать в виде прямоугольников с символом операции внутри. Как показано на том же рисунке 24.1.
Ещё одна важная однокубитная операция - гейт Адамара [H]. Вот матрица это гейта: Особенность этого гейта заключается в том, что он, с одной стороны, превращает определённые состояния кубита |0〉и |1〉 в состояния с максимальной степенью неопределённости: 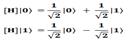А с другой стороны, наоборот, превращает максимально неопределённое состояние в определённое, например:
Воздействие гейта [H] на произвольное однокубитное состояние типа (ф. 24.1) показано на следующей диаграмме:

Нужны, наверное, пояснения. На первом рисунке (считаем слева на право) показано исходное состояние кубита. Второй и последующий рисунки – состояние после воздействия [H]. На третьем рисунке области диаграммы упорядочены. Также заштрихованы «кусочки» группы |1〉 с положительным и отрицательным знаком, которые в силу суперпозиции «съедают» друг друга. На четвёртом рисунке состояние кубита показано уже без этих кусочков. Ну а пятый рисунок просто масштабирован по высоте, чтобы вы могли наглядно сравнить исходное состояние и то, что получилось в результате воздействия.

Дата добавления: 2015-06-04