Алгоритм Шора

Алгоритм Шора — это квантовый алгоритм факторизации (разложения числа на простые множители), позволяющий разложить число N за время O(N3(log N)k), где k=const, затратив O(log N) места.

Значимость алгоритма заключается в том, что при использовании достаточно мощного квантового компьютера, он сделает возможным взлом криптографических систем с открытым ключом. К примеру, RSA использует открытый ключ N, являющийся произведением двух больших простых чисел. Один из способов взломать шифр RSA — найти множители N. При достаточно большом N это практически невозможно сделать, используя известные классические алгоритмы. Так как алгоритм Шора работает только на квантовом компьютере, в настоящее время не существует технических средств, позволяющих за полиномиальное время разложить достаточно большое число на множители. Алгоритм Шора в свою очередь, используя возможности квантовых компьютеров, способен произвести факторизацию числа за полиномиальное время. Это может поставить под угрозу надёжность большинства криптосистем с открытым ключом, основанных на сложности проблемы факторизации чисел.

Как и другие алгоритмы для квантовых компьютеров, алгоритм Шора вероятностный: он даёт верный ответ с высокой вероятностью. Вероятность ошибки может быть уменьшена при повторном использовании алгоритма. Тем не менее, так как возможна проверка предложенного результата (в частности простоты числа) в полиномиальное время, алгоритм может быть модифицирован так, что ответ, полученный в полиномиальное время, будет верным с единичной вероятностью.

Алгоритм Шора был разработан Питером Шором в 1994 году. Семь лет спустя, в 2001 году, его работоспособность была продемонстрирована группой специалистов IBM. Число 15 было разложено на множители 3 и 5 при помощи квантового компьютера с 7 кубитами.
Основные идеи алгоритма Шора 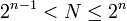Алгоритм Шора основан на возможности быстро вычислить собственные значения унитарного оператора с высокой точностью, если можно эффективно вычислять любые его степени. Взяв в качестве такого оператора умножение на x по модулю N (этот оператор действует в 2n мерном пространстве, где, преобразуя базисный вектор, соответствующий числу a, в базисный вектор, соответствующий числу xa(modN)), мы сможем вычислить такое n, что xn = 1(modN), что позволяет (с высокой вероятностью) разложить N на множители на обычном компьютере.

Дата добавления: 2015-06-04