Условия равновесия произвольной плоской системы сил

Частные случаи приведения плоской системы сил.

В зависимости от значений главного вектора R₀ и главного момента M₀ возможны следующие случаи приведения плоской системы сил.

1) R₀ =0, M₀ =0 - система сил находится в равновесии;

2) R₀ =0, M₀ ≠0 - система эквивалентна паре сил с моментом, равным главному моменту системы, который в этом случае не зависит от выбора центра приведения;

3) R₀ ≠0, M₀ =0 - система эквивалентна равнодействующей R, равной и эквивалентной главному вектору системы R₀, линия действия которой проходит через центр приведения: R = R₀ , R ~ R₀;

4) R₀ ≠ 0, M₀ ≠0 - система эквивалентна равнодействующей R, равной главному вектору системы R₀, ее линия действия проходит на расстоянии d = | M₀ |/ R₀ от центра приведения (рис.20, б).

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M ₀ = 0.

Здесь О - любая точка плоскости.

Из этого условия следуют уравнения равновесия произвольной плоской системы сил, которые можно записать в трех различных формах:

1) Первая форма:

Σ M_A = 0;

Σ X = 0;

Σ Y = 0.

2) Вторая форма:

Σ M_A = 0;

Σ M_B = 0;

Σ Y = 0, где ось Oy неперпендикулярна отрезку АВ.

3) Третья форма:

Σ M_A = 0;

Σ M_B = 0;

Σ M_С = 0, где точки А, В и С не лежат на одной прямой.

Равенства выражают, следующие аналитические условия рав­новесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каж­дую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.

.

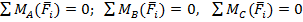Дата добавления: 2015-06-04