Сложение параллельных сил. Центр параллельных сил. Центр системы параллельных сил и центр тяжести

Центр системы параллельных сил и центр тяжести.

Пусть даны две параллельные силы и , направленные в одну сторону и приложенные к точкам и (рис.34).

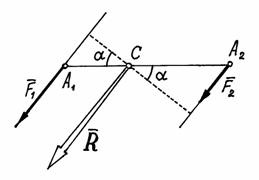
Рис.34

Конечно, величина их равнодейст­вующей . Вектор её параллелен силам и направлен в ту же сторону. С помощью теоремы Вариньона най­дём точку приложения равнодействую­щей – точку С. По этой теореме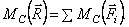

Значит

Отсюда 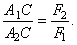То есть точка приложения равнодействующей делит расстояние между точкам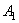и и на части обратно пропорцио­нальные силам.

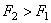Если параллельные силы направ­лены в противоположные стороны (рис.35), то аналогично можно дока­зать, что равнодействующая по вели­чине будет равна разности сил: (если ), параллельна им, направлена в сторону большей силы и расположена за большей силой – в точке С. А расстояния от точки С до точек приложения сил обратно пропорциональны силам: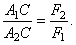

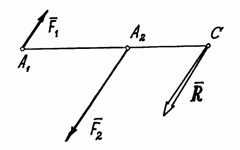
Рис.35

Следует заметить, что если точка приложения равнодействующей располо­жена на одной прямой с точкам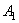и и , точками приложения сил, то, при повороте этих сил в одну сторону на одинаковый угол, рав­нодействующая также повернётся вокруг точки приложе­ния С в том же направлении, и останется параллельной им.

Такая точка приложения равнодействующей называется центром параллельных сил.

Конечно, если хотя бы одну из сил перенести по своей линии дей­ствия в другую точку, то и точка приложения равнодействующей, центр параллельных сил, тоже переместится по линии действия.

Следовательно, положение центра параллельных сил зависит от координат точек приложения сил.

Центром нескольких параллельных сил, найденный последовательным сложением каждых двух сил, будем называть точку С, радиус-вектор которой определяется формулой

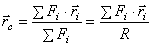, (1)

где 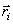- радиусы-векторы точек приложения сил; 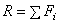– вели­чина равнодействующей параллельных сил, равная алгебраической сумме этих сил (знак силы определяется направлением, которое заранее выбирается и считается положительным).

Используя (1), нетрудно найти координаты центра параллельных сил. Если радиусы-векторы откладывать из начала координат, то проек­ции радиусов-векторов точек на оси будут равны их координатам. По­этому, проектируя векторное равенство (1) на оси, получим

где 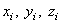– координаты точек приложения сил.

Параллельные силы, распределенные по отрезку прямой.

а) общий случай

- интенсивность распределенной силы [Н/м],

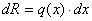- элементарная сила.

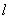– длина отрезка

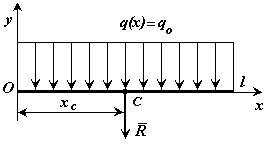
Распределенная по отрезку прямой сила интенсивности эквивалентна сосредоточенной силе .

Сосредоточенная сила прикладывается в точке С (центре параллельных сил) с координатой

б) постоянная интенсивность

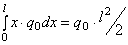
в) интенсивность, меняющаяся по линейному закону

.

Дата добавления: 2015-06-04