Теорема Вариньона.Различные формы условий равновесия плоской системы сил

Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил от­носительно любого центра равен алгеб­раической сумме моментов слагаемых сил относительно того же центра.

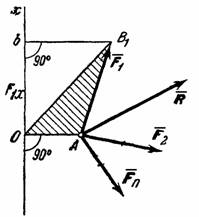
Рис.21

Рассмотрим систему сил 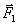, , 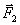…, , 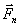сходящихся в точке А (рис.21). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.

Для доказательства теоремы найдем соответствующие выражения моментов m₀(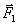), m₀(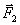), …. По формуле 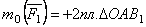. Но, как видно из рисунка, , где F _1x - проекция силы 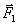на ось Ох; сле­довательно

.

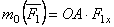Аналогично вычисляются моменты всех других сил.

Обозначим равнодействующую сил 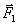, , 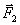…, , 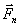через 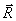, где . Тогда, по теореме о проекции суммы сил на ось, получим . Умножая обе части этого равенства на ОА, найдем:

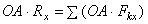
или,

.

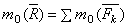Дата добавления: 2015-06-04