Теорема об эквивалентности двухпар сил,расположенных в одной плоскости.Теорема о переносе пары сил в параллельную плоскость

Момент силы относительно точки

Сила, не проходящая через точку крепления тела, вызывает вра­щение тела относительно точки, поэтому действие такой силы на тело оценивается моментом.

Момент силы относительно точки числен­но равен произведению модуля силы на рассто­яние от точки до линий действия силы. Перпен­дикуляр, опущенный из точки на линию дей­ствия силы (рис. 4.4), называется плечом силы. Обозначение момента Mo(F) или mo(F), mo(F) = Fa. Единица измерения [mo(F)] = Н-м.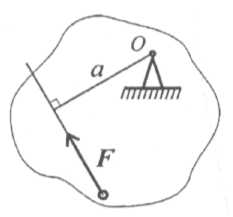

Рис.

Момент считается положительным, если сила разворачивает те­ло по часовой стрелке.

Теорема о переносе пары сил в параллельную плоскость. Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.

Доказательство: Пусть на твердое тело действует пара сил в плоскости. Из точек приложения сил А и В опустим перпендикуляры на плоскость и в точках их пересечения с плоскостью приложим две системы сил и, каждая из которых эквивалентна нулю.

Сложим две равные и параллельные силы и. Их равнодействующая параллель-на этим силам, равна их сумме и приложена посредине отрезка в точке О.

Сложим две равные и параллельные силы и. Их равнодействующая параллель-на этим силам, равна их сумме и приложена посредине отрезка в точке О.

Так как, то система сил эквивалентна нулю и ее можно отбросить.

Таким образом пара сил эквивалентна паре сил, но лежит в другой, параллельной плоскости. Что и требовалось доказать.

Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.

Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.

«Две пары сил, имеющие одинаковые моменты, эквивалентны друг другу, так как путем изменения плеча, модуля сил и перемещения пары сил в плоскости ее действия или переноса этой пары в параллельную плоскость, парысил с одинаковыми моментами могут быть преобразованы одна в другую».

На расчетных схемах обычно вместо пары сил изображают векторный момент 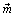, полностью характеризующий ее, при этом модуль 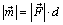. Направление вектора определяет плоскость действия пары и направление поворота в этой плоскости. Чтобы задать пары сил, лежащих в одной плоскости, достаточно обозначить их круговой стрелкой, учитывающей направление поворота, и не изображать сами силы.

Сложение пар сил сводится к теореме о сложении пар: «Система пар сил, действующих на абсолютно твердое тело, эквивалентна одной паре, момент которой равен геометрической сумме моментов слагаемых пар»:

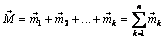. (2.19)

Из приведенной теоремы вытекает условие равновесия системы пар сил, согласно которому для равновесия системы пар сил, действующих на абсолютно твердое тело, необходимо и достаточно, чтобы момент результирующей пары был равен нулю

. (2.20)

Действительно, либо силы результирующей пары равны нулю, либо плечо этой пары равно нулю. В последнем случае силы пары направлены вдоль одной прямой и в соответствии с 1-й аксиомой статики образуют уравновешенную систему сил.

Проецируя векторное равенство (2.20) на координатные оси, получим аналитические условия равновесия системы пар сил:

(2.21)

В частном случае действия на твердое тело системы пар сил, расположенных в одной плоскости, моменты этих пар, направленные по одной прямой, складываются алгебраически. Тогда теорему о сложении парсил формулируют следующим образом: «Система пар сил, лежащих в одной плоскости, эквивалентна одной паре сил, лежащей в той же плоскости и имеющей алгебраический момент, равный алгебраической сумме моментов слагаемых пар»:

. (2.22)

Условия равновесия плоской системы пар сил: «Для равновесия плоской системы пар сил необходимо и достаточно, чтобы алгебраическая сумма моментов этих пар была равна нулю»

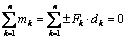. (2.23

7.Векторный момент пары сил.Теорема о сумме моментов сил пары.

Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.

Доказательство: Выберем произвольно точку О. Проведем из нее в точки А и В радиус-векторы (Смотри Рис. 4.2).\

Дата добавления: 2015-06-04