Неподвижный шарнир

Точка крепления пере­мещаться не может. Стер­жень может свободно повора­чиваться вокруг оси шарни­ра. Реакция такой опоры про­ходит через ось шарнира, но неизвестна по направлению. Ее принято изображать в ви­де двух составляющих: гори­зонтальной и вертикальной (R_x\Ry) (рис. 1.11).

Рис. 1.11

Защемление или «заделкам

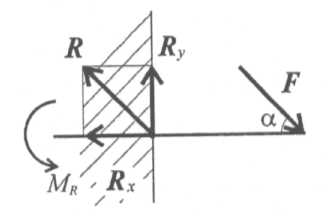
Рис. 1.12

Любые перемещения точки крепле­ния невозможны.

Под действием внешних сил в опоре возникают реактивная сила и реактив­ный момент Mr, препятствующий пово­роту (рис. 1.12).

Реактивную силу принято предста­влять в виде двух составляющих вдоль осей координат

R = R_x + R_y.

Теорема. Действие силы на твердое тело не изменится от переноса силы вдоль своей линии действия.

Пусть в точке А твердого тела приложена сила . К этой силе добавим систему сил, эквивалентную нулю, на ее линии действия, причем (рис.1.13, б). Тогда система сил и , согласно аксиоме 1, зквивалентна нулю, и, согласно аксиоме 2, ее можно отбросить. Получится одна сила , приложенная в точке В (рис.1.13,в).
Сила приложена в точка А. Она эквивалентна такой же по модулю и направлению силе , приложенной в точке В, где точка В - любая точка линии действия силы .
Векторные величины, которые можно прикладывать в любой точке линии действия, называют скользящими. Сила, приложенная к твердому телу, есть вектор скользящий. В деформируемом теле силу нельзя переносить вдоль линии действия. Сила в этом случае не является скользящим вектором.

.

  Рис. 3

3. Система двух непараллельных сил, приложенных в одной точке, эквивалентна одной силе (равнодействующей), приложенной в той же точке и определяемой по правилу параллелограмма (содержание этой аксиомы выражает основное свойство сил, приведенное в лекции 2).

2. Теорема о трех силах. Если (абсолютно твердое) тело находится в равновесии под действием плоской системы трех непараллельных сил (т.е. сил, из которых хотя бы две непараллельные), то линии их действия пересекаются в одной точке.

Доказательство. Пусть из трех сил F 1, F 2, F ₃, приложенных соответственно в точках А, В и С (рис.3), непараллельными являются F 1 и F 2. Продолжим линии их действия до пересечения в точке О и перенесем в эту точку обе силы. Очевидно, система { F 1, F 2} эквивалентна 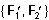, а эта последняя уже имеет равнодействующую R. Таким образом,

{ F 1, F 2, F 3} { R, F 3,}. (3)

Но система двух сил находится в равновесии только в том случае, если они направлены вдоль одной прямой. Следовательно, линия действия F 3 должна совпасть с линией действия R, т.е. пройти через точку О.

3)

Система сил, линии действия которых пе­ресекаются в одной точке, называется сходя­щейся (рис. 2.1).

Необходимо определить равнодействую­щую системы сходящихся сил (F₁; F₂; F₃; …; F_n ), n — число сил, входящих в систему.

По следствию из аксиом статики, все си­лы системы можно переместить вдоль линии действия, и все силы окажутся приложенными в одной точке.

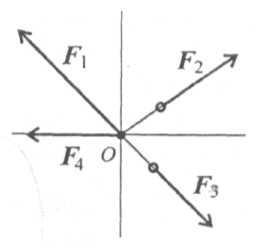
Рис.

Дата добавления: 2015-06-04