Центр тяжести тел. На все точки тела, находящегося вблизи поверхности Земли, дей­ствуют силы – силы тяжести этих точек или их вес

На все точки тела, находящегося вблизи поверхности Земли, дей­ствуют силы – силы тяжести этих точек или их вес 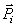. Вообще эти силы будут сходящимися – линии действия их пересекаются в центре Земли. Но, если пренебречь размерами тела в сравнении с размерами Земли, то можно считать их параллельными.

Центр этих параллельных сил, сил тяжести точек, называется цен­тром тяжести тела.

Значит находить центр тяжести тел можно как центр параллельных сил. Например, координаты его

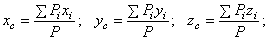(2)

где 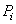– вес каждой точки тела, а 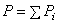– вес всего тела.

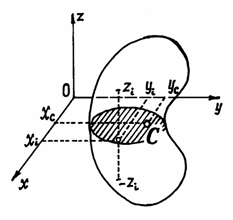
Рис.36

При определении центра тяжести полезны несколько теорем.

1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой плоско­сти.

Если оси х и у расположить в этой плоскости симметрии (рис.36), то для каждой точки с координатами 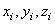можно отыскать точку с координатами 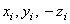. И координата 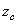по (2), бу­дет равна нулю, т.к. в сумме 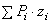все члены имеющие противоположные знаки, попарно уничтожаются. Значит центр тяжести расположен в плоскости симметрии.

2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Действительно, в этом случае, если ось z провести по оси симмет­рии, для каждой точки с координатами 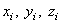можно отыскать точку с координатами 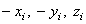и координаты 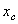и 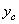, вычисленные по фор­мулам (2), окажутся равными нулю.

Аналогично доказывается и третья теорема.

3) Если однородное тело имеет центр симметрии, то центр тя­жести тела находится в этой точке.

И ещё несколько замечаний.

Первое. Если тело можно разделить на части, у которых известны вес и положение центра тяжести, то незачем рассматривать каждую точку, а в формулах (2) 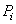– определять как вес соответствующей части и 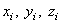– как координаты её центра тяжести.

Второе. Если тело однородное, то вес отдельной части его 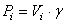, где 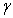- удельный вес материала, из которого сделано тело, а 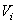- объём этой части тела. И формулы (1) примут более удобный вид. Например,

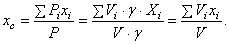
И аналогично, 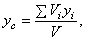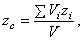где 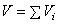- объём всего тела.

Третье замечание. Если тело состоит из однородных пластин одинаковой, малой толщины, то объём каждой пластины 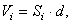где 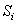– площадь пластины, d – толщина. И координаты центра тяжести будут определяться только с по­мощью площадей:

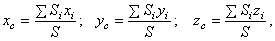
где 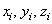– координаты центра тяжести отдельных пластин; – общая площадь тела.

Четвёртое замечание. Если тело состоит из стержней, прямых или кри­волинейных, однородных и постоянного сечения, то вес их 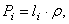где l_i – длина, – вес единицы длины (погонного метра), а координаты центра тяжести будут определяться с помощью длин отдельных участков:

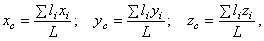
где 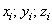– координаты центра тяжести 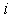-го участка;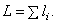

Отметим, что согласно определению центр тя­жести - это точка геометрическая; она может лежать и вне преде­лов данного тела (например, для кольца).

15.Способы задания движения точки.Определение скорости и ускорения точки при различных способах задания ее движения.
Способы задания движения точки

Для задания движения точки можно применять один из следую­щих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор 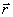, проведенный из на­чала координат О в точку М (рис. 1).

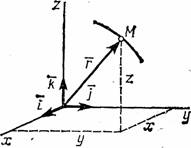
Рис.1

При движении точки М вектор 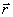будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, 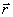является переменным вектором (вектором-функцией), зависящим от аргу­мента :

.

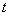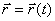Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор 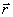и найти положение движущейся точки.

Геометрическое место концов вектора 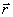, т.е. годограф этого вектора, определяет траекторию движущейся точки.

2. Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.1), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости

, , .

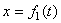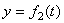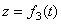Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

Чтобы получить уравнение траектории надо из уравнений движения исключить параметр .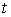

Нетрудно установить зависимость между векторным и координатным способами задания движения.

Разложим вектор 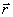на составляющие по осям координат:

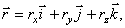
где 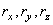- проекции вектора на оси; 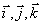– единичные векторы направленные по осям, орты осей.

Так как начало 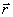вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому

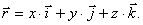
3. Естественный способ задания движе­ния точки.

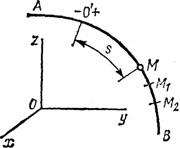
Рис.3

Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.3) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Тогда положение точки М на тра­ектории будет однозначно определяться криволинейной коорди­натой s, которая равна расстоянию от точки О' до точки М, изме­ренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M ₁, М ₂,.... следовательно, расстояние s будет с течением времени изменяться.

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость

.

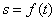Уравнение выражает закон движения точки М вдоль тра­ектории.

Определение скорости точки при координатном способе задания движения

Вектор скорости точки 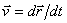, учитывая, что 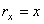, , 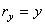, 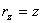найдем:

, , .

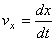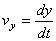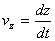Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.

Зная проекции скорости, найдем ее модуль и направление (т.е. углы 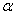, , 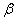, 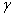которые вектор 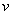образует с координатными осями) по формулам

;

, , .

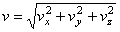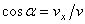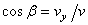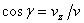Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени.

Направлен вектор скорости по касательной к траектории, кото­рая нам наперед известна.

Определение скорости точки при естественном способе задания движения

Величину скорости можно определить как предел (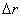 – длина хорды ):

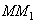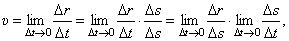
где 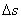– длина дуги 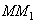. Первый предел равен единице, второй предел – производная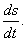

Следовательно, скорость точки есть первая производная по времени от закона движения:

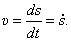
Направлен вектор скорости, как было установлено ранее, по касательной к траектории. Если величина скорости в данный момент будет больше нуля, то вектор скорости направляется в положительном направлении

Определение ускорения при координатном способе задания движения

Вектор ускорения точки 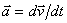в проекции на оси получаем:

, ,

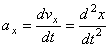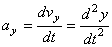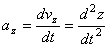
или

, , ,

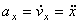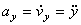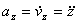т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул

;

, , ,

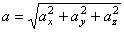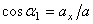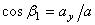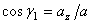где 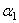, , 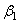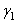- углы, образуемые вектором ускорения с координатными осями.

Пример 3. Движение точки задано уравнениями .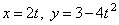

Из первого уравнения 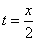. Подставив во второе, получим уравнение траектории: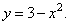

Это уравнение параболы. В на­чале движения, при 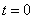, точка находи­лась на самом верху, в положении M ₀ ().

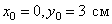А, например, при t =0,5 c она будет в положении M с координатами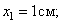

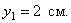
Проекции скорости на оси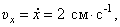

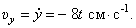
При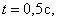

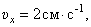
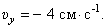
И модуль скорости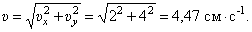

Составляющие скорости по осям и вектор её показаны в масштабе на рис. 7.

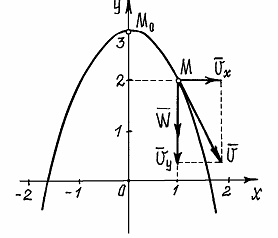
Рис.7

Проекции ускорения 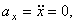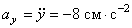. Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрица­тельна, то вектор ускорения на­правлен верти­кально вниз, и величина его постоянна, не за­висит от времени.

Определение ускорения при естественном способе задания движения. Касательное и нормальное ускорение точки

При естественном способе задания движения вектор 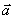определяют по его проекциям на оси 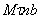, имеющие начало в точке М и движущиеся вместе с нею (рис.8). Эти оси, называемые осями естественного трехгранника (или скоростными (естественными) осями), направлены следующим образом: ось 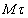- вдоль каса­тельной к траектории в сторону положительного отсчета расстояния s; ось 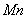- по нормали, лежащей в соприкасающейся плос­кости и направленной в сторону вогнутости траектории; ось 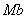- перпендикулярно к первым двум так, чтобы она образовала с ними правую тройку. Нормаль 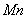, лежащая в соприкасающейся плоскости(вплоскости самой кривой, если кривая плоская), называетсяглавной нормалью, а перпендикулярная к ней нормаль 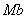- бинормалью.

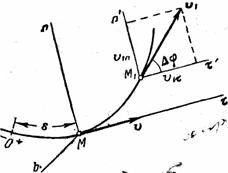
Рис.8

Было показано, что ускорение точки 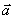лежит в соприкасающейся плоскости, т.е. в плоскости 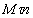; следовательно, проекция вектора 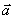на бинормаль равна нулю ().

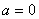Вычислим проекции 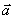, на две другие оси. Пусть в моментвремени t точка находится в положении М и имеет скорость 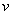, a в момент 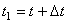приходит в положение М ₁ и имеет скорость .

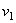Тогда по определению

.

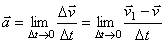Перейдем в этом равенстве от векторов к их проекциям на ос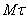и и 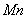, проведенные в точке М (рис.8). Тогда на основании теоремы о проекции суммы (или разности) векторов на ось получим:

, .

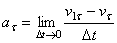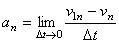Учитывая, что проекция вектора на параллельные оси одинаковы, проведем через точку М ₁ оси 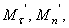параллельные 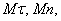и обозначим угол между направлением вектора 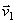и касательной 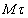через 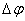. Этот угол между касательными к кривой в точках М и М ₁ называется углом смежности.

Напомним, что предел отношения угла смежности 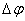к длине дуги 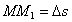определяет кривизну k кривой в точке М. Кривизна же является величиной, обратной радиусу кривизны 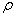в точке М. Таким образом,

.

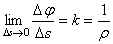Обращаясь теперь к чертежу (рис.9), находим, что проекции векторов 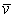и 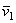на оси 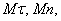будут равны:

,

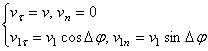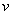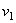где и - численные величины скорости точки в моменты 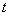и .

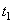Следовательно,

.

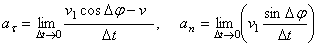Заметим что при 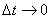точка М ₁ неограниченно приближается к М и одновременно

.

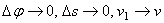Тогда, учитывая, что в пределе 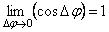, получим для 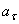выражение

.

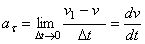Правую часть выражения 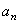преобразуем так, чтобы в нее вошли отношения, пределы которых нам известны. Для этого умножим числитель и знаменатель дроби, стоящей под знаком предела, на 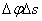. Тогда будем иметь

,

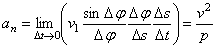так как пределы каждого из стоящих в скобке сомножителей при 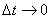равны:

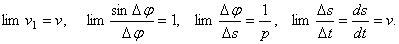
Окончательно получаем:

.

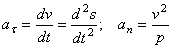Итак, мы доказали, что проекция ускорения точки на каса­тельную равна первой производной от численной величины скорости или второй производной от расстояния (криволинейной координаты) s noвремени, а проекция ускорения на главную нормаль равна квадрату скорости деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинор­маль равна нулю (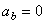). Эти результаты выражают собою одну из важных теорем кинема­тики точки.

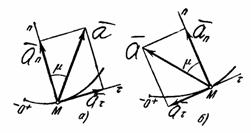
Рис.9

Отложим вдоль касатель­ной 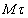и главной нормали 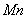векторы 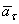и 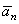, чис­ленно равные 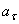и 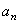(рис. 9). Эти векторы изображают касательную и нормальную составляющие ускорения точки. При этом составляющая 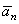бу­дет всегда направлена в сторону вогнутости кривой (величина a всегда положительна), а составляющая 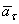может быть направлена или в положительном, или в отрицательном направлении оси 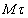в зависимости от знака проек­ции 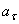(см. рис.9, а и б).

Вектор ускорения точки 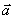изображается диагональю параллело­грамма, построенного на составляющих 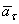и 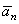. Так как эти состав­ляющие взаимно перпендикулярны, то по модулю:

.

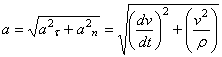Дата добавления: 2015-06-04