Длина пути резания

Гребнистость дна борозды

Высота гребешков определяется координатами точки В (рис. 4.3):

,

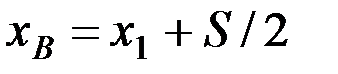где х_В - абсцисса вершины гребешка В;

х₁ - абсцисса кромки ножа при ωt₁+90°.

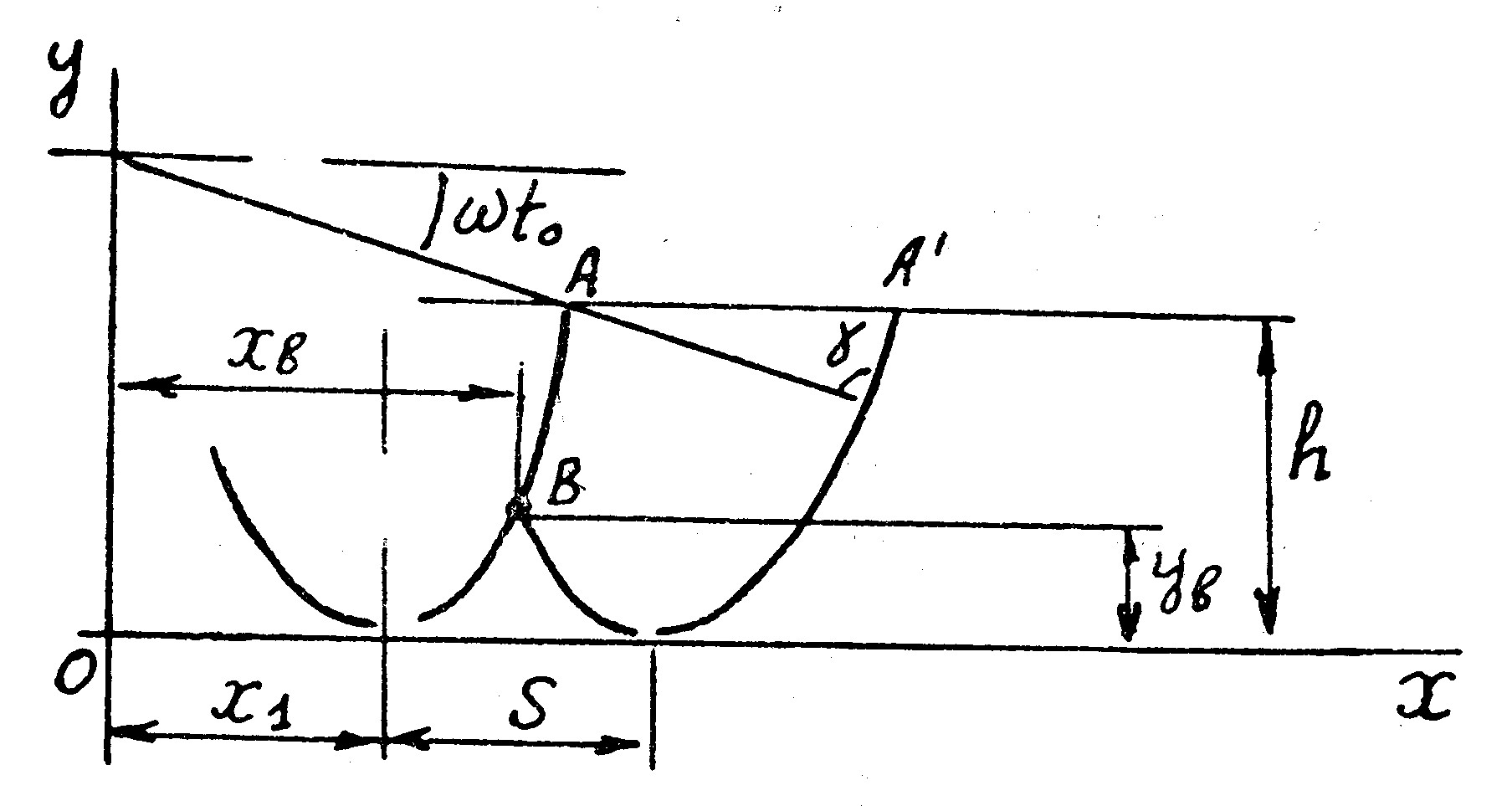
Рис. 4.3. Схема определения толщины стружки и гребнистости дна борозды

Из параметрических уравнений трохоиды (4.1) следует

;

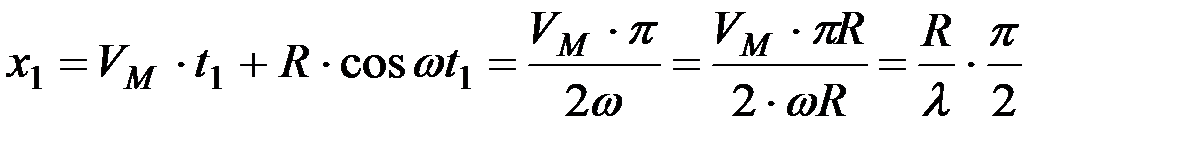ранее определенное значение S (4.3):

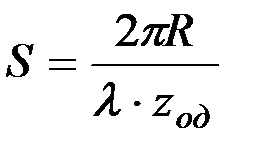; или .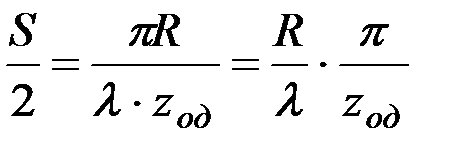

Подставляя х₁ и S/2 в уравнение х_В можно получить:

.

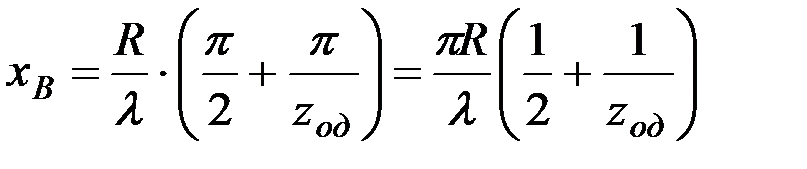Если значение y_B обозначить как с (высота гребешков), то подставляя х_В и у_В в уравнение (4.2а), получим

;

или, если учесть, что

,

можно найти

.

Из этого уравнения можно найти высоту гребешков С, если известны параметры фрезы и λ, но чаще его используют для определения кинематического показателя λ, исходя из допустимого значения высоты гребешков с_доп:

,

тогда

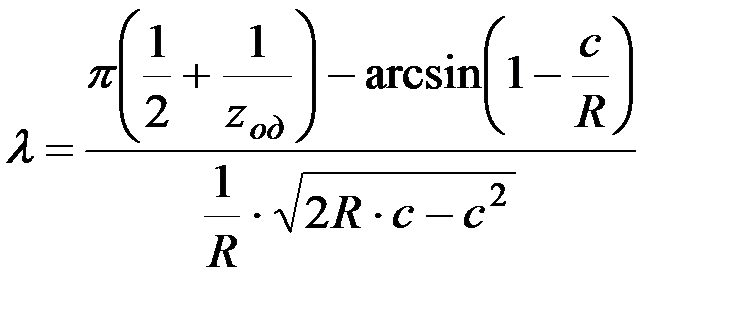. (4.5)

Под длиной пути резания стружки понимают длину отрезка трохоиды от поверхности поля до точки пересечения двух соседних траекторий в нижней части (точка В, рис. 4.3).

От длины пути резания в значительной мере зависят затраты энергии на процесс фрезерования. Чем меньше длина пути резания, тем меньше (при прочих равных условиях) работа на отрезание стружки и тем самым энергия, затрачиваемая на технологический процесс.

Элемент дуги траектории может быть определен как

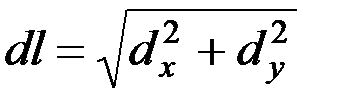. (4.6)

Поскольку

;

,

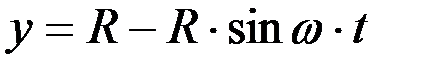то

; ;

; ,

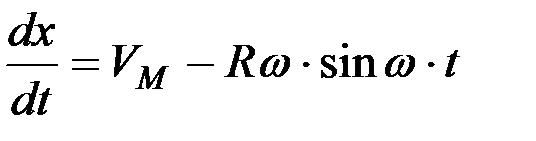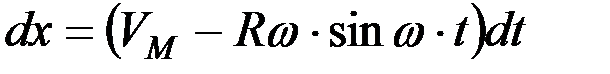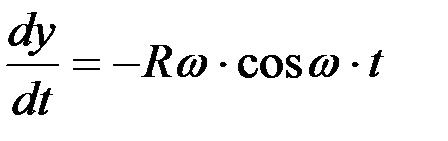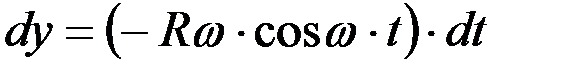или

; ,

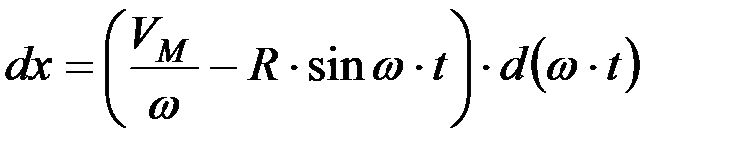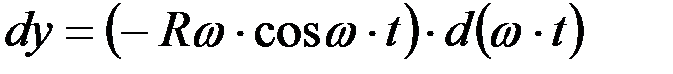тогда

.

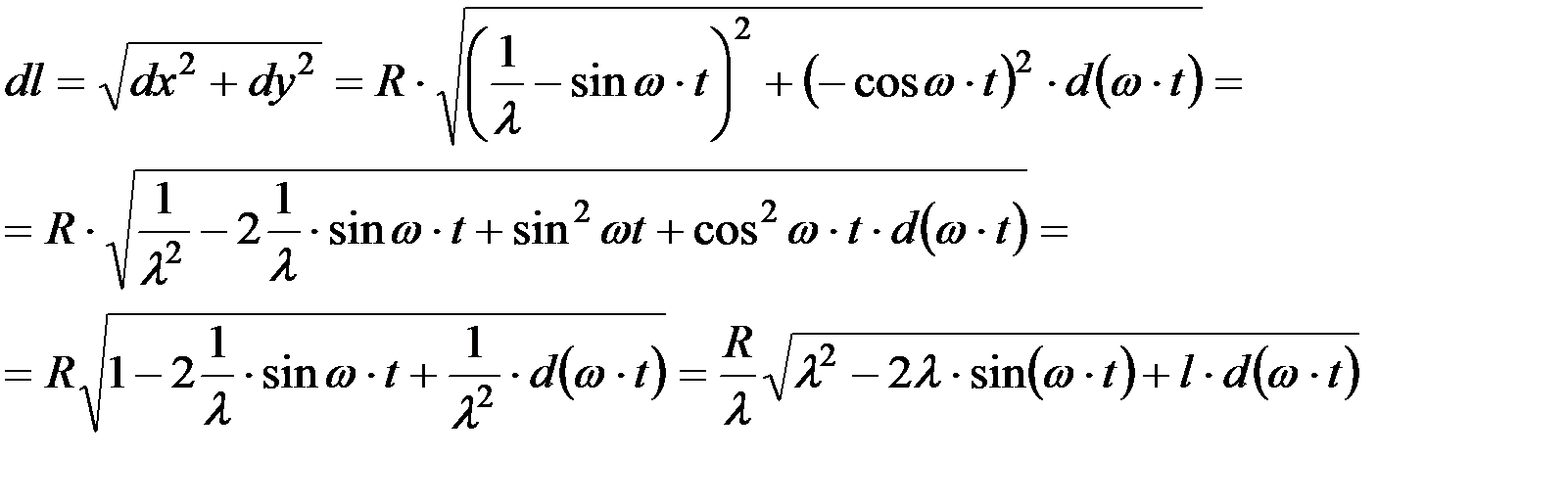Если ввести обозначения

ωt = α; ωt₁ = α; ωt₂ = α,

где α₁ - угол наклона ножа к горизонту при входе в почву;

α₂ - угол наклона ножа к моменту конца резания стружки, то

.

Данный интеграл относится к типу эллиптических интегралов второго рода, и его определение представляет определенную трудность.

Угол α₁ определяется из соотношения

, (4.8)

а угол

. (4.9)

При наличии ЭВМ значительно проще произвести численное решение интеграла, например, по методу Симпсона с любой точностью.

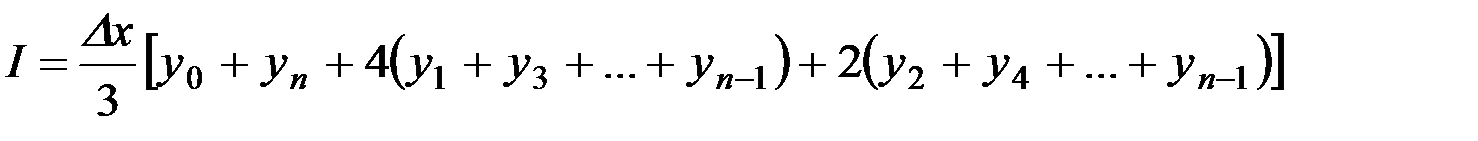, (4.10)

где Δх - шаг приращения аргумента при численном интегрировании;

y_i - значение функции при фиксированном аргументе.

Вычисления длины пути резания позволяют проследить влияние различных параметров (R,λ,z) на энергетические показатели технологического процесса

Дата добавления: 2015-06-04