Устойчивость сошника

На неравномерность глубины заделки семян существенное влияние оказывает устойчивость хода сошника по глубине, которая обусловлена величиной действующих на него сил (рис. 9.7).

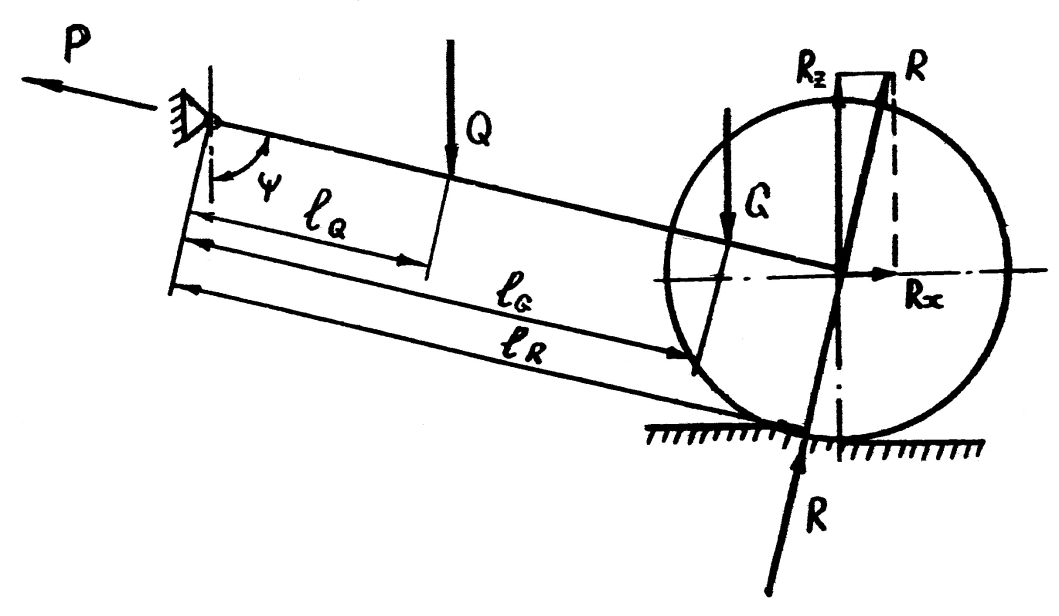
Рис. 9.7. Расчетная схема дискового сошника

Если в целях упрощения считать, что сила тяжести сосредоточена в центре массы сошника, силы сопротивления почвы заменить равнодействующей R, силу давления пружины Q считать вертикальной, а силу тяги сошника Р по направлению совпадающей с поводком, то обычными условиями устойчивости сошника в статике являются

,

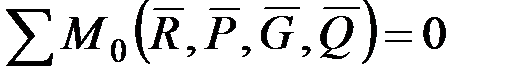. (9.19)

В качестве критерия устойчивости движения сошника может быть принято постоянство угла наклона поводка, что будет наблюдаться при отсутствии колебаний сошника. В этом случае статическое равновесие сошника может быть описано только уравнением моментов сил относительно оси подвеса.

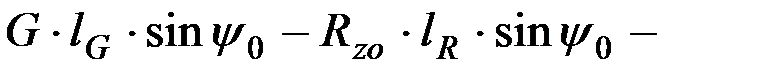
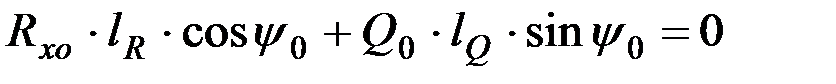, (9.20)

где l_G, l_R, l_Q - расстояния от оси подвеса сошника) до точек приложения соответствующих сил;

ψ ₀ - угол наклона сошника при статическом равновесии.

Статическое равновесие сошника может наступить лишь при наличии с однородной почвы с ровным микрорельефом и движении агрегата с постоянной скоростью. Поскольку это невыполнимо, и все силы меняются, то равновесие сошника постоянно нарушается, и он колеблется около оси подвеса. В этом случае условие статического равновесия (9.20) должно обеспечить выполнение хотя бы среднего значения заданной глубины заделки семян.

Действительный характер движения сошника может быть описан дифференциальным уравнением, составленным, например, с использованием принципа Д, Аламбера [6]:

, (9.21)

где I - момент инерции сошника относительно оси подвеса.

При достаточно жестких современных требованиях к неравномерности заделки семян в почву отклонения сошника от установившегося среднего положения можно считать достаточно малыми, т.е.

,

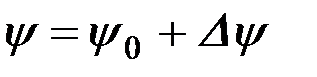причем

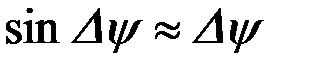, а 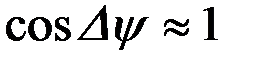. (9.22)

Силы, действующие на сошник, также можно представить в виде суммы некоторого среднего значения и переменных, мгновенных приращений:

,

,

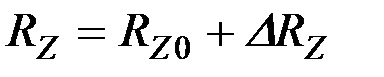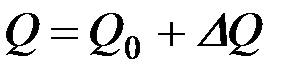. (9.23)

Подставляя значения сил и угла колебаний в исходное дифференциальное уравнение (9.21), можно получить

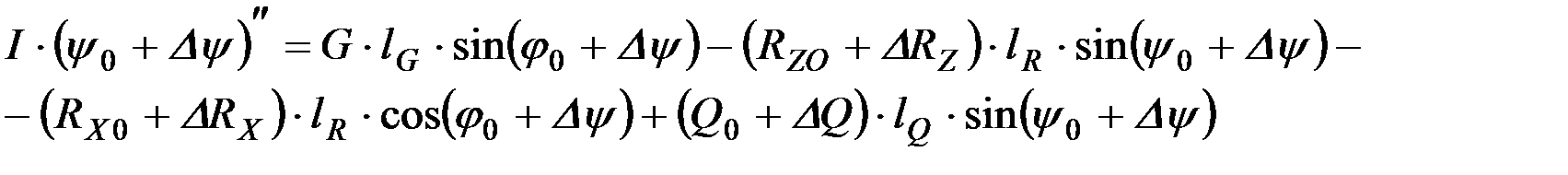
Если развернуть значение синуса и косинуса суммы двух углов, то

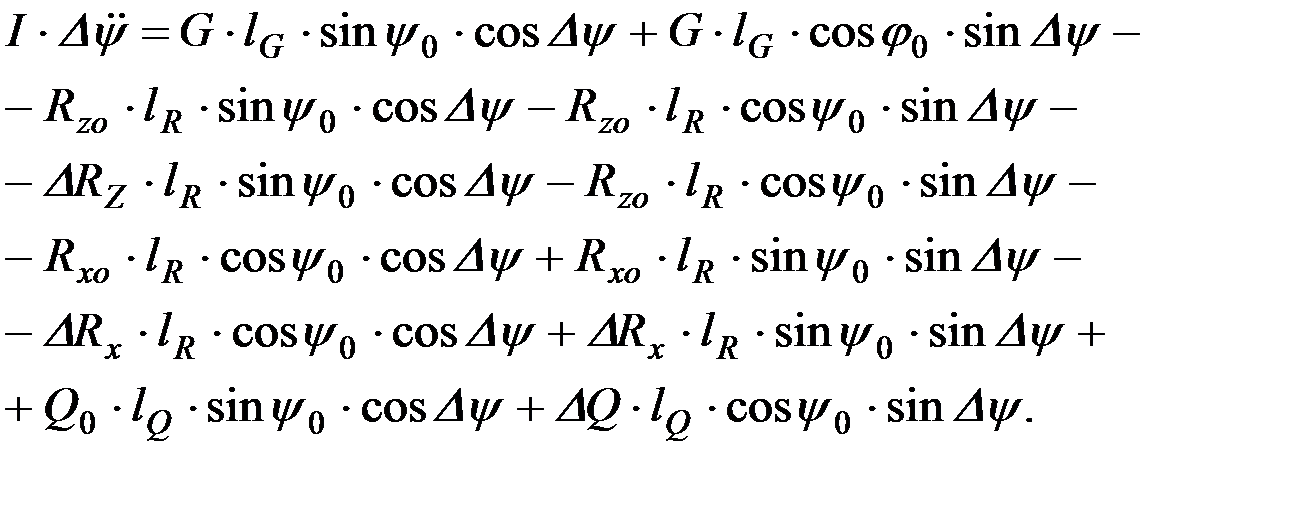
С учетом свойств малых углов (9.22) уравнение может быть упрощено:

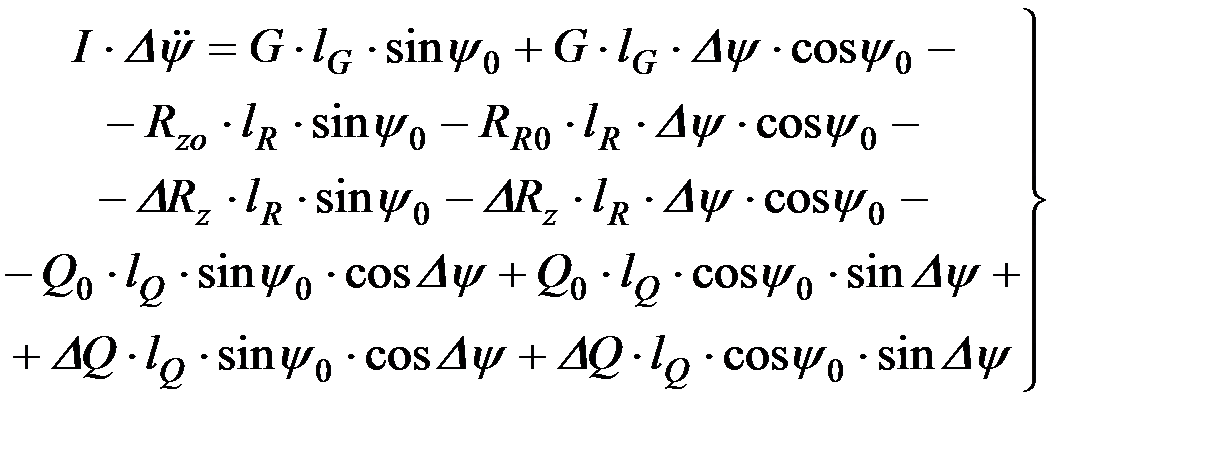Малые второго порядка

Сумма слагаемых этого уравнения, подчеркнутых прямой чертой, представляет собой условие статического равновесия (9.20) и, стало быть, равна нулю. Слагаемые, подчеркнутые волнистой линией, включают произведение двух малых величин ΔR_z, ΔR_x, ΔQ и Δψ, т.е. являются малыми второго порядка.

С учетом этого

Если постоянную, которая заключена в скобки, обозначить величиной А, то

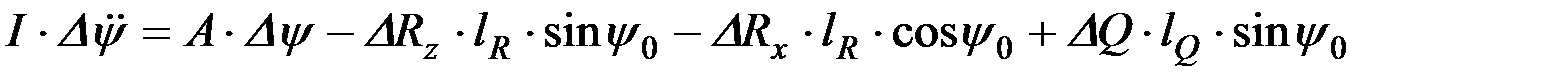. (9.24)

Сопротивление почвы R_x, R_z и сила сжатия пружины Q зависят, в свою очередь, от угла наклона сошника. В самом деле, если сошник заглубить, то есть уменьшить ψ, то сопротивление почвы возрастает. Изменится при этом и сила сжатия пружины Q. Но указанные силы будут зависеть еще и от скорости движения агрегата, а следовательно, и интенсивности изменения угла колебаний сошника.

Известно, что при увеличении скорости сеялки сошники "всплывают", и это обстоятельство обязательно учитывают при подготовке скоростной сеялки к работе.

Кроме того, эти силы непрерывно изменяются во времени, так как сеялка движется по полю, а микрорельеф его представляет собой случайную функцию. Не остается постоянной твердость почвы и другие ее физико-механические свойства.

Таким образом,

(9.25)

Вид этих зависимостей может быть очень сложен. Полезные результаты от их использования получают обычно путем линеаризации. В данном случае линеаризация усложнена тем, что зависимость этих функций от времени является случайной, а, следовательно, не всегда дифференцируемой.

В таких случаях, как известно, проводят неполную линеаризацию с помощью формулы Тейлора, т.е. зависимость от ψ и ψ¢ принимают линейной, а зависимость от t оставляют в том виде, в каком она проявляется в действительности:

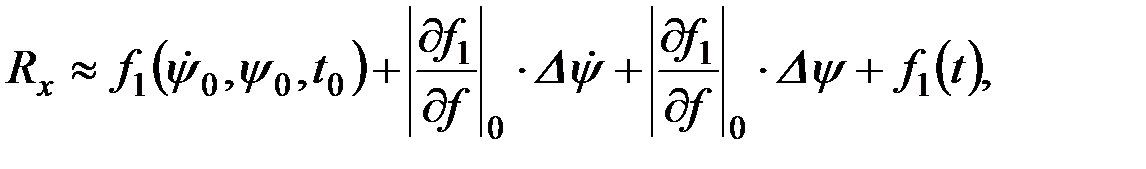
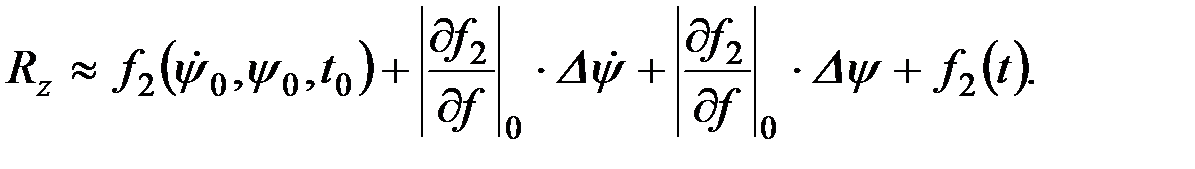
В этом уравнени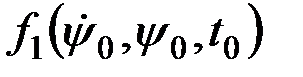и и 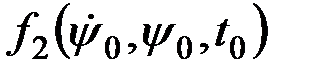являются значениями функций при нулевых начальных условиях, т.е. в положении начального статистического равновесия, а

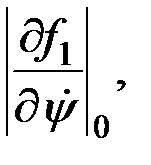
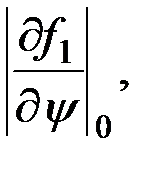
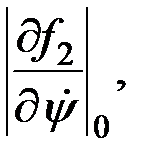
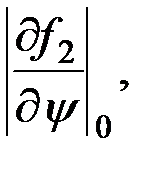
- постоянными коэффициентами, так как частные производные вычислены около конкретного, нулевого значения функции.

Если рассмотреть отклонения значений функции ΔR_x и ΔR_z, то

,

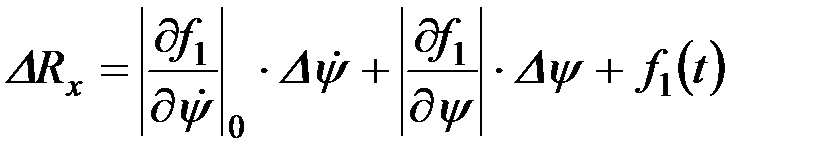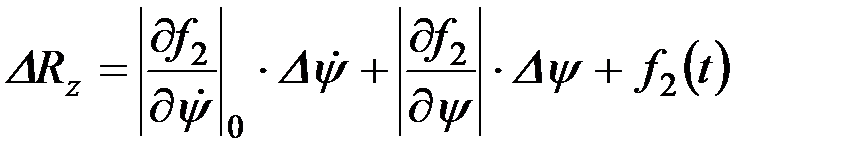. (9.26)

Приращение силы сжатия пружины ΔQ составит:

,

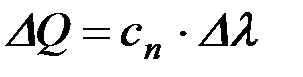где Δλ - величина деформации пружины;

с_n - жесткость пружины.

Поскольку

,

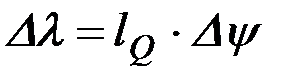то

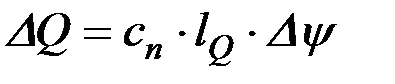. (9.27)

Найденные значения ΔR_x ΔR_z и ΔQ можно подставить в уравнение (9.24):

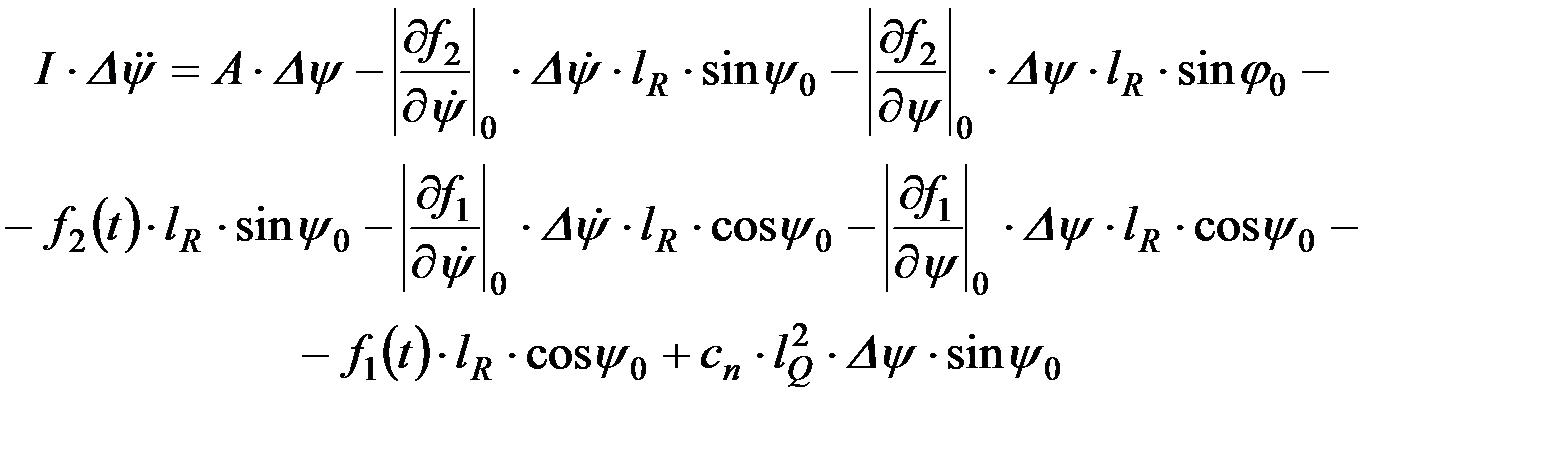
После приведения подобных членов и введения обозначений постоянных величин

;

.

,

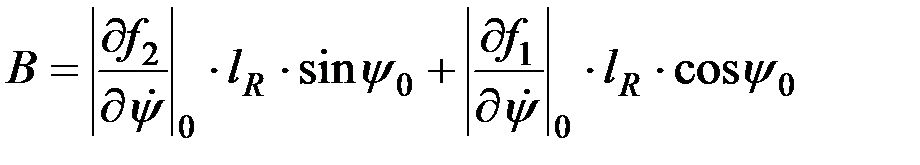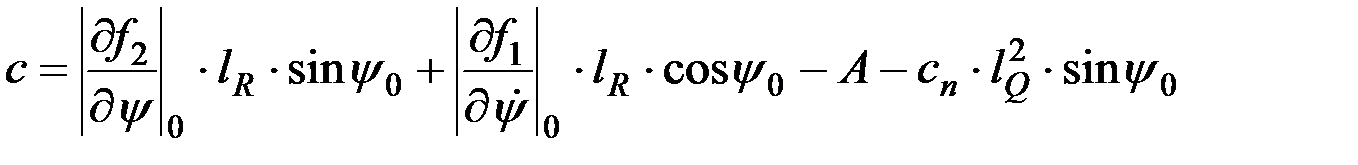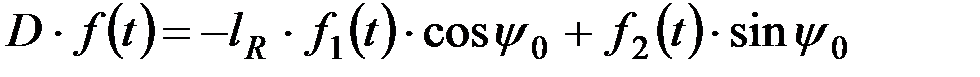где Df(t) - обобщенная функция внешних возмущений, можно получить .

Если еще раз изменить обозначения, то можно уравнение малых колебаний сошника представить в следующем виде:

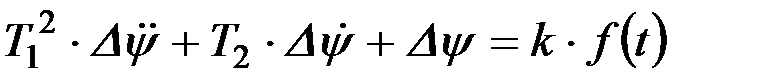, (9.28)

где

, , .

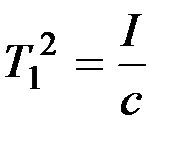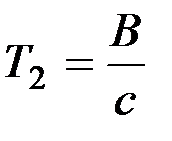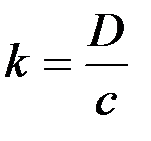Коэффициенты Т₁ и Т₂ характеризуют инерционные и демпфирующие свойства сошника при движении его в почве, к - коэффициент усиления системы. Заметим, что коэффициенты Т₁, Т₂ и к зависят от параметров конструкции сошника - его размеров, массы, момента инерции, силы давления пружины.

Дата добавления: 2015-06-04