Характеристика функций внешних возмущений, действующих на механическую систему в условиях нормального функционирования

В этом случае, когда на вход системы воздействует вполне определенные возмущения, которые могут быть описаны простыми детермированными функциями, выходные параметры могут быть определены с помощью передаточной функции (9.34).

Но задача значительно усложняется тем, что функция внешних возмущений обычно оказывается случайной, т.е. такой, которая в результате опыта может принять тот или иной вид, причем неизвестно заранее, какой именно. Примером такого воздействия могут быть неровности поверхности поля, изменения твердости почвы и т.п.

Очень часто случайные функции внешних возмущений имеют вид непрерывных случайных колебаний около некоторого среднего значения, причем ни средняя амплитуда, ни характер этих колебаний не обнаруживают существенных изменений с течением времени. Такие случайные функции называют стационарными. Если аргументом таких функций является время, то их называют еще случайными процессами.

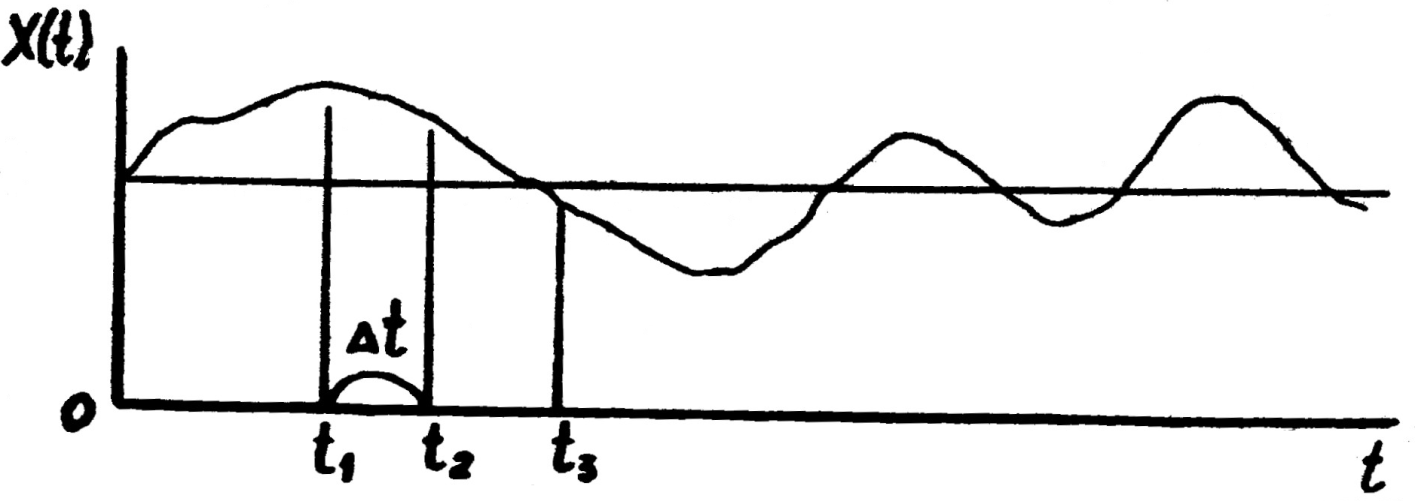
Рис. 9.18. Стационарный случайный процесс

Основными характеристиками стационарной случайной функции, как известно, являются корреляционная функция и функция спектральной плотности [6,8,9].

Корреляционная функция характеризует связь между значениями случайной функции, относящимися к различным моментам времени, отстоящими друг от друга на расстоянии τ:

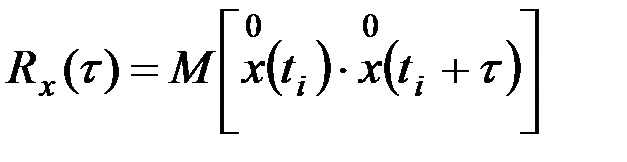, (9.39)

где 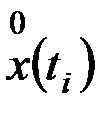; 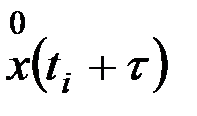- центрированные значения случайного процесса;

;

.

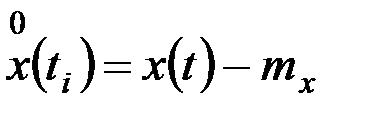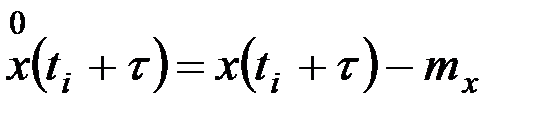Таким образом, для стационарного случайного процесса корреляционная функция определяется средней величиной произведения центрированнных ординат, отстоящих друг от друга на расстоянии τ (рис. 9.19).

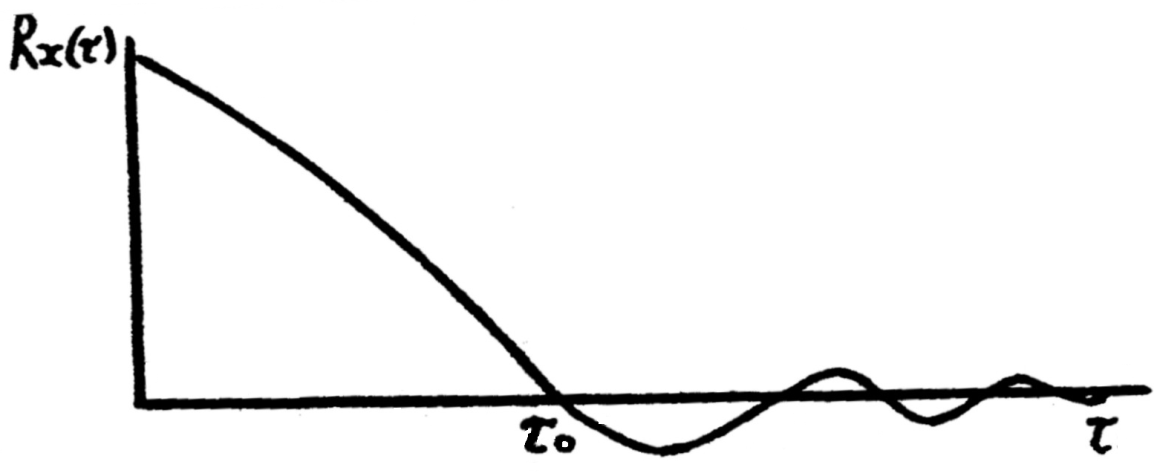
Рис. 9.19. Корреляционная функция

Отрезок τ₀ определяет среднюю величину времени, при котором сохраняется корреляционная связь между ординатами.

Если случайный процесс представляет собой некоторую плавно изменяющуюся функцию, то τ₀ может принять достаточно большое значение. У быстропротекающих резкоизменяющихся процессов τ₀ оказывается малой величиной. Если R_x(τ) разделить на величину дисперсии D_x этого же процесса, то в результате может быть получена нормирования корреляционная функция ρ_х(τ), которая меняется лишь от 0 до 1 при любых пределах изменения R_x(τ):

.

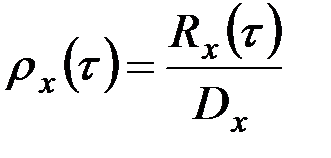Представление о частотном составе случайного процесса можно получить с помощью функции спектральной плотности σ(τ), которая представляет собой косинус-преобразование Фурье от значений корреляционной функции (рис. 9.20);

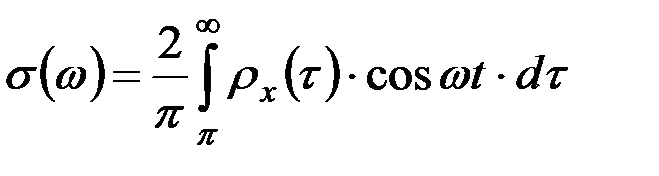, (9.40)

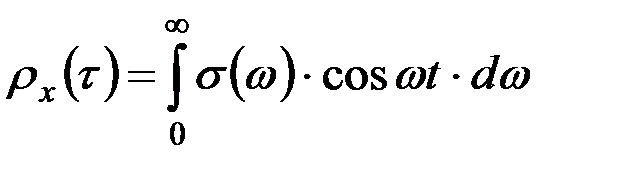. (9.41)

Рис. 9.20. График спектральной плотности

Функция спектральной плотности описывает спектр частот, образующих случайный процесс. Чем более широк спектр частот, тем более беспорядочен случайный процесс.

Помимо определения корреляционной функции и спектральной плотности отдельно от входного X(t) и выходного Y(t) процессов, можно находить значения взаимной корреляционной функции и спектральной плотности этих процессов:

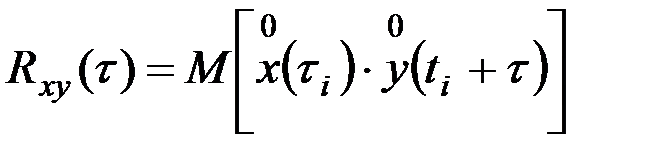, (9.42)

т.е. взаимная корреляционная функция определяется математическим ожиданием средней величины произведения нормированных ординат входного и выходного процессов, отстоящих друг от друга на расстоянии τ.

Так как R_xy(τ) не является четной функцией, то ее нужно вычислять не только для положительных, но и для отрицательных значений τ:

,

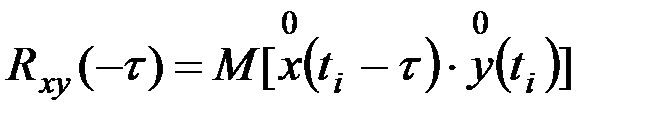или, что то же самое,

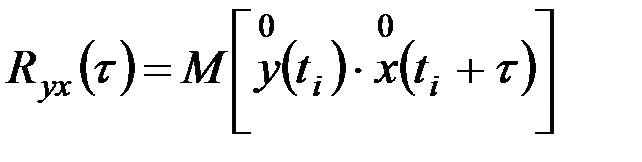. (9.43)

Вычисление нормированных оценок взаимной корреляционной функции производится по уравнениям

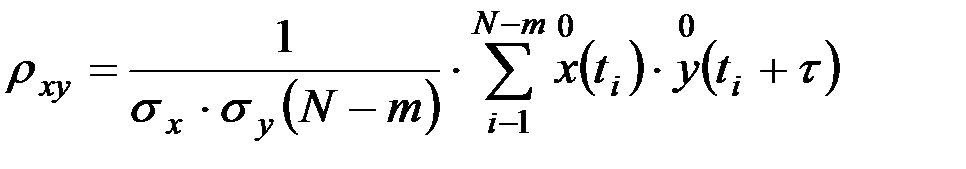; (9.44)

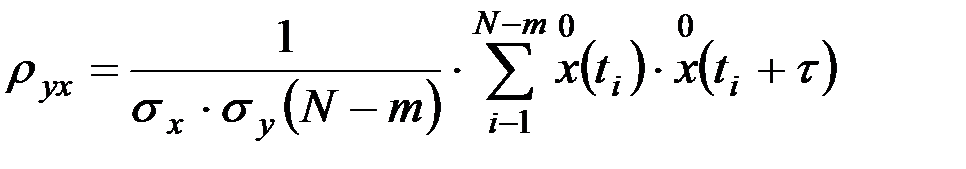. (9.45)

где N - число ординат в анализируемой реализации случайного процесса;

m - число коэффициентов корреляционной функции.

В отличие от взаимной корреляционной функцию обычную, определяемую по уравнению (9.39), иногда называют автокорреляционной и обозначают R_xx(τ) или ρ_xx(τ).

Для конкретной реализации стационарных случайных процессов X(t) и Y(t) взаимная спектральная плотность S_xy(w) определяется как прямое преобразование Фурье взаимной корреляционной функции:

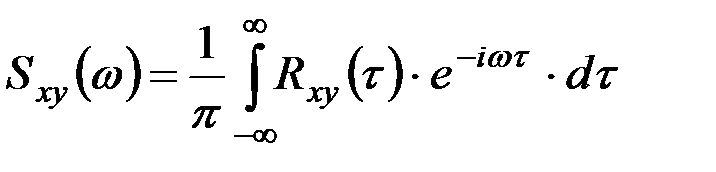. (9.45,а)

Взаимная спектральная плотность является комплексной функцией аргумента - частоты ω, поэтому

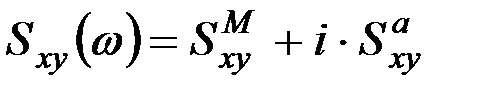, (9.46)

где 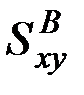и 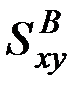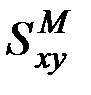- соответственно вещественная и мнимая части взаимной спектральной плотности.

Поскольку в соответствии с известной формулой Эйлера

,

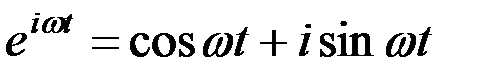то вещественная часть 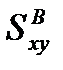вычисляется как косинус-преобразование, а мнимая 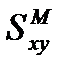как синус-преобразование Фурье:

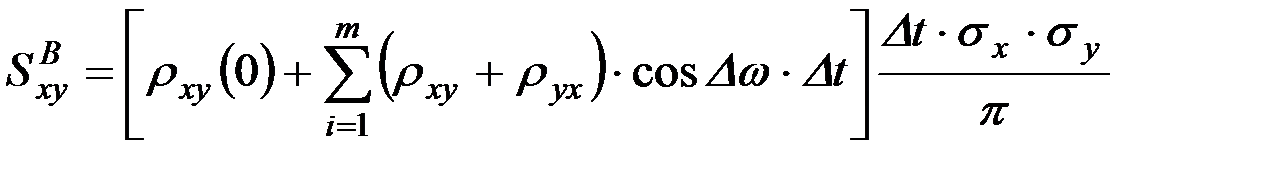, (9.47)

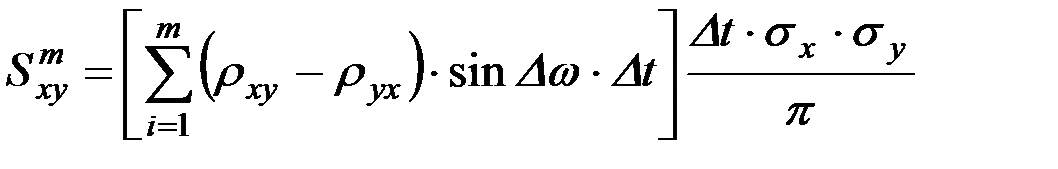, (9.48)

где Δt - промежуток времени между двумя соседними ординатами в реализации изучаемого случайного процесса (рис. 9.14);

Δω - шаг изменения частоты.

Нормированная взаимная спектральная плотность определяется из формулы:

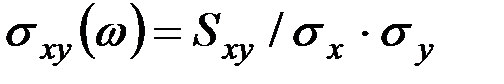, (9.49)

где σ_х и σ_у - среднеквадратические отклонения реализации случайных процессов.

Как всякое комплексное число, взаимная спектральная плотность может быть представлена в виде вектора с модулем

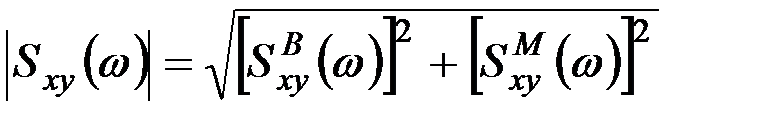(9.50)

и углом фазового сдвига

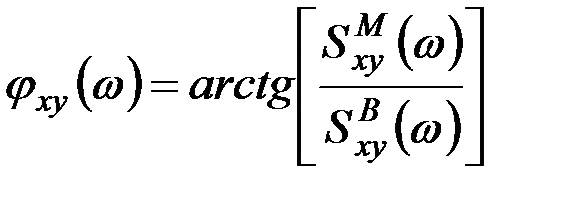. (9.51)

Характеристики стационарно й случайной функции внешних возмущений преобразуются линейными динамическими системами сельскохозяйственных машин.

Пусть на вход линейной динамической системы (т.е. системы, описываемой линейными дифференциальными уравнениями) поступает стационарная функция X(t) с характеристиками m_x, R_x(τ), S_x(σ) (рис. 9.21).

Реакция системы будет представлять собой случайную функцию Y(t). Поскольку характеристиками случайных функций являются неслучайные функции m_x, R_x(τ), S_x(σ) и m_y, R_y(τ), S_y(σ) (рис. 9.21).

Реакция системы будет представлять собой случайную функцию Y(t). Поскольку характеристиками случайных функций являются неслучайные функции m_x, R_x(τ), S_x(σ) и m_y, R_y(τ), S_y(ω), то прежде всего можно рассмотреть задачу об определении реакции системы на неслучайные воздействия f(t). Линейное дифференциальное уравнение колебаний сошника (9.29) в этом случае можно представить как

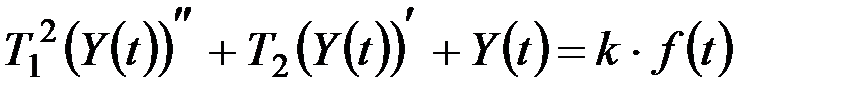. (9.52)

В случае, когда f(t) является достаточно простой аналитической функцией, реакцию системы довольно часто можно найти в виде аналогичной функции. В частности, если f(t) - простое гармоническое колебание, то система (как ранее уже было рассмотрено - рис. 9.13) отвечает также гармоническим колебанием, но с измененной амплитудой и сдвинутым по фазе. Входное гармоническое колебание может быть описано так:

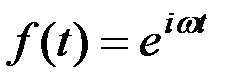. (9.53)

Реакцию системы Y(t) можно представить тоже в виде гармонического колебания, но умноженного на некоторый комплексный множитель:

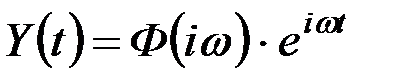. (9.54)

Для того, чтобы определить, что представляет собой комплексный множитель Ф(iω), необходимо значения Y(t) и f(t) подставить в дифференциальное уравнение (9.52):

.

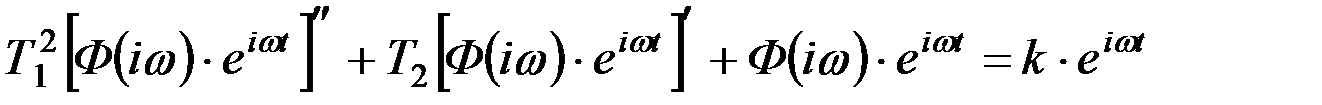После дифференцирования, деления левой и правой частей уравнения на е^iωt и вынесения Ф(iω) за скобки можно получить

,

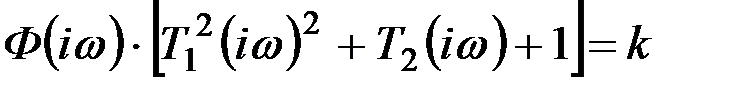откуда

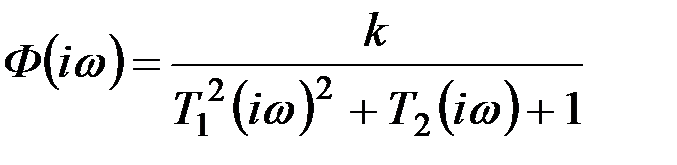. (9.55)

Но это нечто иное, как частотная функция линейной динамической системы.

Таким образом, если на вход линейной динамической системы поступает гармоническое колебание того же вида 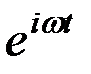, то на выходе окажется гармоническое колебание того же вида, умноженное на частотную характеристику системы.

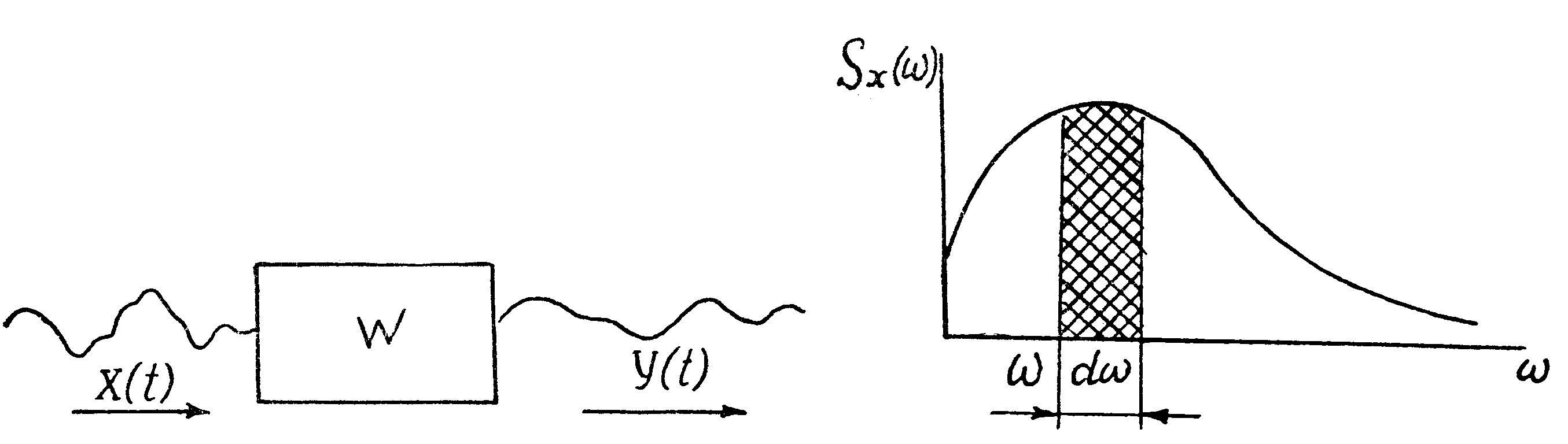
Рис. 9.21. Динамическая модель сошника при случайных входных и выходных функций	Рис. 9.22. Спектральная плотность случайного процесса

Спектральная плотность входного и выходного случайных процессов представляет собой разложение дисперсии по отдельным частотам.

В самом деле, можно записать по аналогии (9.40) и (9.41):

,

.

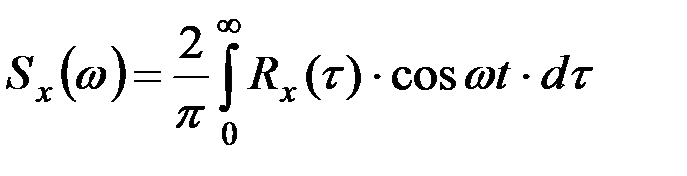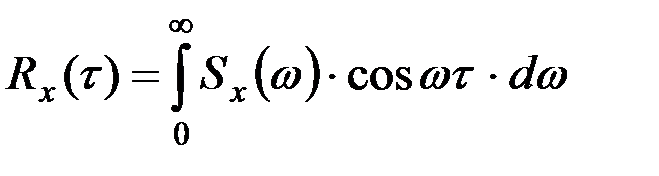Если τ=0, то последнее уравнение может быть представлено как

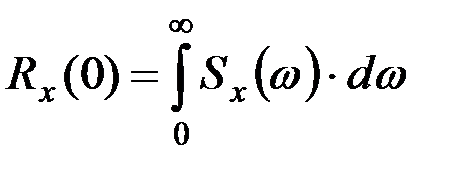. (9.56)

Но согласно (9.39)

.

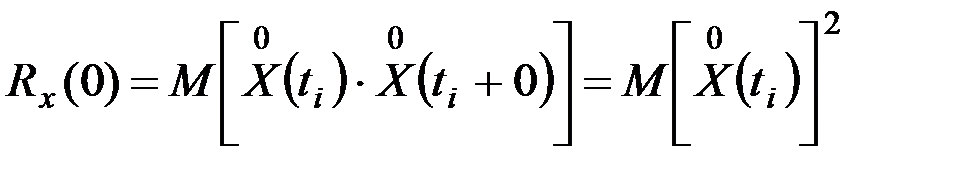Поскольку математическое ожидание квадрата отклонения центрированных значений случайной величины - это дисперсия D_x, то площадь 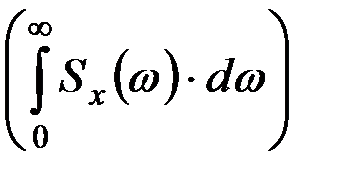, заключенная между кривой функции спектральной плотности и осью абсцисс (рис. 9.22), равна D_x.

Произведение любой ординаты S_x(ω) на dω геометрически представляет собой прямоугольник, составляющий часть D_x, т.е. определяет вклад в общую дисперсию D_x колебаний системы с частотой ω.

Каждой гармонике входного процесса можно привести в соответствие выходное колебание с той же частотой, но измененное по амплитуде и сдвинутое по фазе или, в общей случае, умноженное на частотную функцию W(iω) по уравнению (9.55).

Частотная функция как комплексное число (рис. 9.12) может быть представлена в виде вектора с модулем A(ω) и углом сдвига фаз φ(ω). Если связать все элементарные участки дисперсии S_x(ω)dω входной и выходной функции спектральной плотности, то можно получить

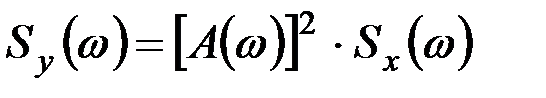, (9.57)

так как дисперсия определяется квадратом случайной величины.

Уравнение (9.57) может явиться основой для построения экспериментальной кривой квадрата модуля частотной функции

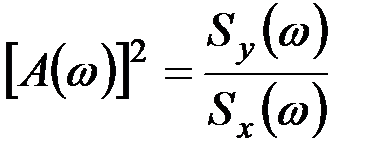. (9.58)

Поскольку уравнение частотной функции сошниковой группы известно (9.21)

,

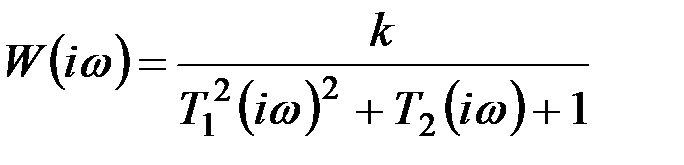то квадрат модуля частотной функции

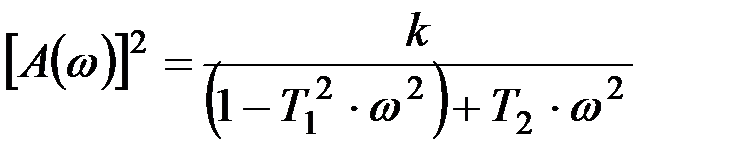. (9.59)

Если на экспериментальной кривой квадрата модуля частотной функции взять значения 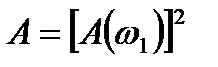и 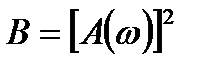для двух значений частот ω₁ и ω₂, а также определить к при ω=0, то для определения коэффициентов передаточной функции необходимо решить систему уравнений второго порядка:

,

,

,

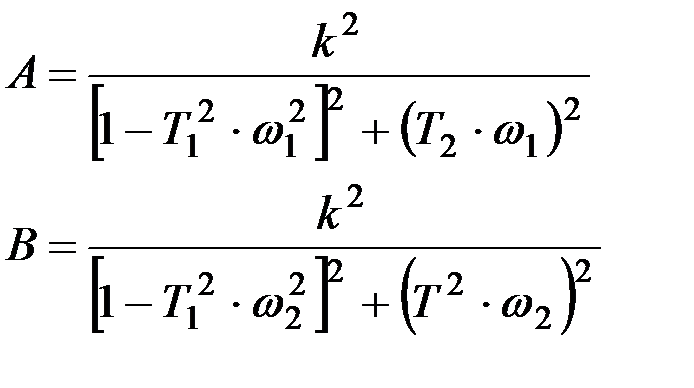
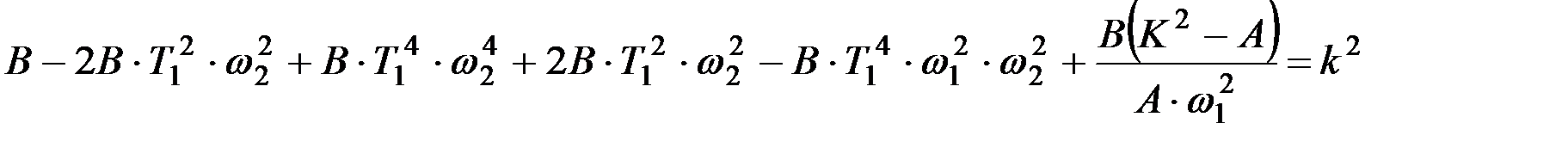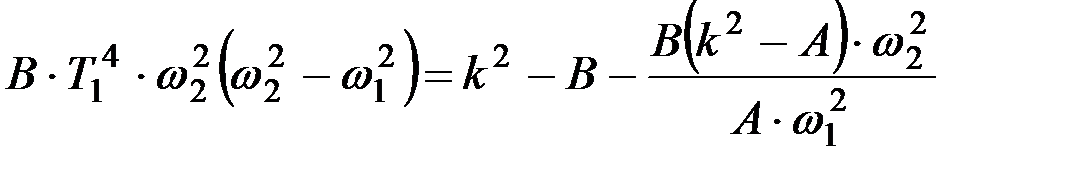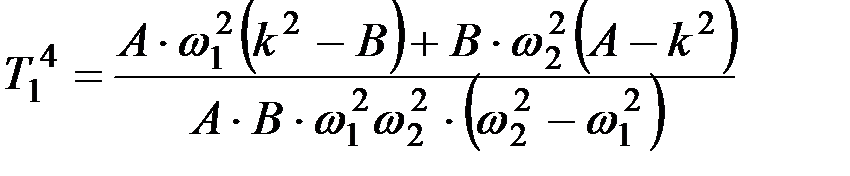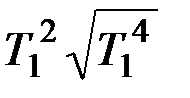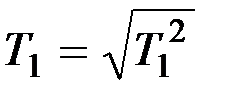; , (9.60)

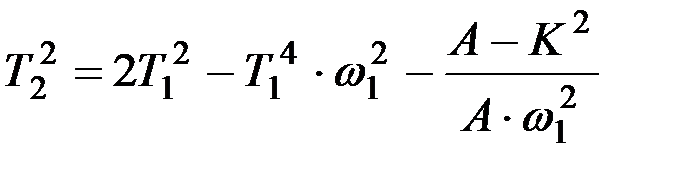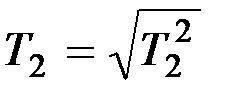, . (9.61)

После определения к, Т₁, Т₂ находят теоретическое значение функции 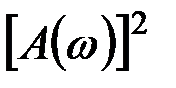по уравнению (9.59). Если теоретическая и экспериментальная кривые достаточно близки друг к другу, то коэффициенты передаточной функции можно считать определенными. В случае значительного отличия теоретической и экспериментальных кривых берут другие значения А и В и повторяют расчет.

Опыт определения коэффициентов этим методов [9] показал, что ошибки при этом оказываются большими и он рекомендуется лишь для тех случаев, когда X(t) и Y(t) слабо коррелированы. При достаточно высоком уровне корреляции между входными и выходными процессами одномерной модели экспериментальные значения амплитудно-частотной характеристики рекомендуется вычислять по выражению

, (9.62)

а коэффициент усиления -

. (9.63)

В этом случае экспериментальные значения А, В, ω₁, ω₂ необходимо взять на кривой, построенной по уравнению (9.62). Если в результате расчета окажется, что по соотношению Т₁ и Т₂ сошник будет представлять собой колебательное звено (Т₂‹2Т₁), то необходимо изменить его параметры (момент инерции, силу сжатия пружины, размеры) так, чтобы перевести в апериодическое звено второго порядка. Зависимости коэффициентов от параметров конструкций, полученные при выводе уравнения малых колебаний сошников (9.28), позволяют провести целенаправленное изменение коэффициентов передаточной функции.

9.8. Возможности компьютерной программы "Сеялка, (Sejlka)" при анализе работы посевных машин

Программа "Сеялка", разработанная на кафедре сельскохозяйственных машин, позволяет определить технологические показатели, необходимые для настройки сеялки и оценки ее динамических свойств при работе в условиях непрерывных случайных возмущений.

Предварительный выбор длины рабочей части высевающей катушки и передаточного числа механизма привода можно произвести с помощью диаграммы высева, построенной на экране дисплея, а затем определить число зубьев сменных звездочек на схеме механизма привода, обеспечивающего это передаточное отношение.

Далее рассчитываются данные, необходимые для настройки сеялки в полевых условиях.

Процесс заделки семян в почву определяется динамическими свойствами сошника и качеством подготовки почвы к посеву.

Программа предусматривает вычисление коэффициентов корреляционной функции и спектральной плотности профиля поверхности поля и угла колебаний, записанных синхронно при испытании работы сеялки на заданной скорости движения агрегата. результаты могут быть представлены в форме графиков и таблиц. Характеристики случайной функции вычисляются дважды - без фильтрации ординат и с фильтрацией по текущему среднему значению.

Динамические свойства определяются коэффициентами передаточной функции, которые рассчитываются по соотношению значений спектральной плотности входного X(t) и выходного Y(t) процессов. Далее предусматривается выбор длины маркеров и следоуказателя, обеспечивающих заданную величину стыкового междурядья.

На экране дисплея осуществляется мультипликация движения посевного агрегата с рассчитанными параметрами маркеров, что позволяет проверить правильность стыковки соседних проходов.

Контрольные вопросы

1. Как обеспечивают надежное поступление семян из семенного ящика к высевающим аппаратам?

2. Как определить рабочий объем высевающей катушки, при котором обеспечивается требуемая норма высева семян при тои или ином междурядье?

3. Что называют приведенной толщиной активного слоя семян?

4. Как определить действительную толщину активного слоя семян?

5. Каким должен быть зазор между катушкой и донышком высевающего аппарата?

6. Как используют сведения о предсошниковых холмах при проектировании сеялки?

7. Для какой цели в сошниках устанавливают семянаправительные пластинки?

8. Как составляют дифференциальное уравнение движения сошника сеялки?

9. Что представляет собой уравнение малых колебаний сошника?

10. Что представляет собой и для каких целей используется передаточная функция той или иной динамической системы, в частности сошника сеялки?

11. Какими свойствами обладают передаточные функции динамических систем?

12. Что представляют собой частотные функции динамических систем?

13. Что представляют собой переходные функции динамических систем?

14. Что представляют собой функции внешних возмущений, воздействующих на рабочие органы сеялки в условиях нормального функционирования?

15. Какими оценками характеризуют случайные функции?

16. Что представляет собой корреляционная функция и как ее построить на основе экспериментальных данных?

17. Как характеризует случайный процесс функция спектральной плотности?

18. Как преобразуются характеристики случайных функций внешних возмущений линейными динамическими системами машин.

Литература

1. Кошурников А.Ф. и др. Анализ технологических процессов, выполняемых сельскохозяйственными машинами, с помощью ЭВМ. Пермь, 1995 - 272 с.

2. Турбин Б.Г. и др. Сельскохозяйственные машины. Л. Машиностроение, 1967.

3. Лурье А.Б. и др. Сельскохозяйственные машины. СПб, 1998, - 366 с.

Дата добавления: 2015-06-04